Ta đã biết công thức tính thể tích của khối cầu bán kính R là \(V=\dfrac{4\pi R^3}{3}\). Làm thế nào để tìm ra công thức đó?
Ta đã biết công thức tính thể tích của khối cầu bán kính R là \(V=\dfrac{4\pi R^3}{3}\). Làm thế nào để tìm ra công thức đó?

Gọi d là đồ thị của hàm số y = f(x) = 6 – 2x. Kí hiệu S1 là diện tích hình phẳng giới hạn bởi d, trục hoành và trục tung, S2 là diện tích hình phẳng giới hạn bởi d, trục hoành và đường thẳng x = 5 (Hình 1).
a) Tính S1 và so sánh với \(\int\limits^5_3f\left(x\right)dx\).
b) Tính S2 và so sánh với \(\int\limits^5_3f\left(x\right)dx\).
c) So sánh \(\int\limits^5_0\left|f\left(x\right)\right|dx\) với S1 + S2.
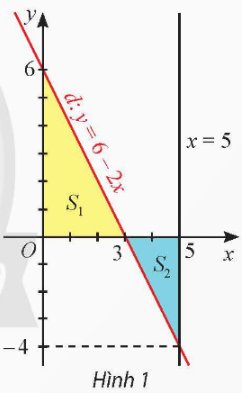
Thảo luận (1)Hướng dẫn giảia) Tam giác \(OAB\) vuông tại \(O\), ta có \(OA = 6\), \(OB = 3\). Diện tích tam giác \(OAB\) là:
\({S_1} = \frac{{OA.OB}}{2} = \frac{{6.3}}{2} = 9\).
Ta có \(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_0^3 {\left( {6 - 2x} \right)dx} = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 = 9 - 0 = 9\).
Như vậy \({S_1} = \int\limits_0^3 {f\left( x \right)dx} \)
b) Tam giác \(CBM\) vuông tại \(M\), ta có \(MB = 2\), \(MC = 4\). Diện tích tam giác \(CBM\) là:
\({S_2} = \frac{{MB.MC}}{2} = \frac{{2.4}}{2} = 4\).
Ta có \(\int\limits_0^3 {f\left( x \right)dx} = \int\limits_3^5 {\left( {6 - 2x} \right)dx} = \left. {\left( {6x - {x^2}} \right)} \right|_3^5 = 5 - 9 = - 4\).
Như vậy \({S_2} = - \int\limits_3^5 {f\left( x \right)dx} \)
c) Ta có:
\(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = \int\limits_0^5 {\left| {6 - 2x} \right|dx} = \int\limits_0^3 {\left| {6 - 2x} \right|dx} + \int\limits_3^5 {\left| {6 - 2x} \right|dx} = \int\limits_0^3 {\left( {6 - 2x} \right)dx} + \int\limits_3^5 {\left( {2x - 6} \right)dx} \)
\( = \left. {\left( {6x - {x^2}} \right)} \right|_0^3 + \left. {\left( {{x^2} - 6x} \right)} \right|_3^5 = \left( {9 - 0} \right) + \left[ {\left( { - 5} \right) - \left( { - 9} \right)} \right] = 13\)
Như vậy \(\int\limits_0^5 {\left| {f\left( x \right)} \right|dx} = 13 = {S_1} + {S_2}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = 2x – x2, trục hoành và hai đường thẳng x = 0, x = 3.
Thảo luận (1)Hướng dẫn giảiDiện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = 2x - {x^2}\), trục hoành và hai đường thẳng \(x = 0\), \(x = 3\) là \(S = \int\limits_0^3 {\left| {2x - {x^2}} \right|dx} \)
Ta có \(2x - {x^2} = 0 \Leftrightarrow x = 0\) hoặc \(x = 2\).
Với \(x \in \left[ {0;2} \right]\) thì \(2x - {x^2} \ge 0\). Với \(x \in \left[ {2;3} \right]\) thì \(2x - {x^2} \le 0\).
Vậy \(S = \int\limits_0^3 {\left| {2x - {x^2}} \right|dx} = \int\limits_0^2 {\left( {2x - {x^2}} \right)dx} + \int\limits_2^3 {\left( {{x^2} - 2x} \right)dx} \)
\( = \left. {\left( {{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 + \left. {\left( {\frac{{{x^3}}}{3} - {x^2}} \right)} \right|_2^3 = \left( {\frac{4}{3} - 0} \right) + \left[ {0 - \left( { - \frac{4}{3}} \right)} \right] = \frac{8}{3}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tính diện tích hình phẳng giới hạn bởi đồ thị của hàm số y = cosx – 2, trục hoành và hai đường thẳng x = 0, x = π.
Thảo luận (1)Hướng dẫn giảiDiện tích hình phẳng giới hạn bởi đồ thị của hàm số \(y = \cos x - 2\), trục hoành và hai đường thẳng \(x = 0\), \(x = \pi \) là \(S = \int\limits_0^\pi {\left| {\cos x - 2} \right|dx} \).
Do \(\cos x - 2 < 0\) với \(\forall x \in \left[ {0;\pi } \right]\).
Do đó \(S = \int\limits_0^\pi {\left( {2 - \cos x} \right)dx} = \left. {\left( {2x - \sin x} \right)} \right|_0^\pi = 2\pi - 0 = 2\pi \).
(Trả lời bởi Nguyễn Quốc Đạt)
Cho hai hàm số y = 4x – x2 và y = x lần lượt có đồ thị (P) và d như Hình 4.
a) Tính diện tích S1 của hình phẳng giới hạn bởi (P), trục hoành và hai đường thẳng x = 0, x = 2.
b) Tính diện tích S của hình phẳng giới hạn bởi (P), d và hai đường thẳng x = 0, x = 2.
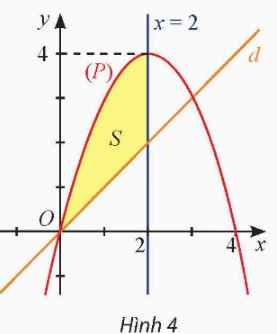
Thảo luận (1)Hướng dẫn giải
Diện tích \({S_1}\) của hình phẳng giới hạn bởi \(\left( P \right)\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_1} = \int\limits_0^2 {\left| {4x - {x^2}} \right|dx} \)
Ta thấy rằng với \(\forall x \in \left[ {0;2} \right]\) thì \(4x - {x^2} \ge 0\), do đó:
\({S_1} = \int\limits_0^2 {\left( {4x - {x^2}} \right)dx} = \left. {\left( {2{x^2} - \frac{{{x^3}}}{3}} \right)} \right|_0^2 = \frac{{16}}{3}\)
b) Diện tích \({S_2}\) của hình phẳng giới hạn bởi \(d\), trục hoành và hai đường thẳng \(x = 0\), \(x = 2\) là \({S_2} = \int\limits_0^2 {\left| x \right|dx} \).
Ta thấy rằng với \(\forall x \in \left[ {0;2} \right]\) thì \(x \ge 0\), do đó:
\({S_2} = \int\limits_0^2 {xdx} = \left. {\left( {\frac{{{x^2}}}{2}} \right)} \right|_0^2 = 2\)
Vậy diện tích \(S\) của hình phẳng giới hạn bởi \(\left( P \right)\), \(d\) và hai đường thẳng \(x = 0\), \(x = 2\) là \(S = {S_1} - {S_2} = \frac{{16}}{3} - 2 = \frac{{10}}{3}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = x2 – 2x – 1, y = x – 1 và hai đường thẳng x = 1, x = 4.
Thảo luận (1)Hướng dẫn giảiDiện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = {x^2} - 2x - 1\), \(y = x - 1\) và hai đường thẳng \(x = 1\), \(x = 4\) là:
\(S = \int\limits_1^4 {\left| {\left( {{x^2} - 2x - 1} \right) - \left( {x - 1} \right)} \right|dx} = \int\limits_1^4 {\left| {{x^2} - 3x} \right|dx} \)
Ta có \({x^2} - 3x = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\)
Do đó
\(S = \int\limits_1^3 {\left| {{x^2} - 3x} \right|dx} + \int\limits_3^4 {\left| {{x^2} - 3x} \right|dx} = \left| {\int\limits_1^3 {\left( {{x^2} - 3x} \right)dx} } \right| + \left| {\int\limits_3^4 {\left( {{x^2} - 3x} \right)dx} } \right|\)
\( = \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_1^3} \right| + \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_3^4} \right| = \left| {\frac{{ - 9}}{2} - \frac{{ - 7}}{6}} \right| + \left| {\frac{{ - 8}}{3} - \frac{{ - 9}}{2}} \right| = \left| { - \frac{{10}}{3}} \right| + \left| {\frac{{11}}{6}} \right| = \frac{{31}}{6}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Tính diện tích hình phẳng giới hạn bởi đồ thị của hai hàm số y = 5x − x2, y = x2 – x và hai đường thẳng x = 0, x = 2.
Thảo luận (1)Hướng dẫn giảiDiện tích hình phẳng giới hạn bởi đồ thị của hai hàm số \(y = 5x - {x^2}\), \(y = {x^2} - x\) và hai đường thẳng \(x = 0\), \(x = 2\) là
\(S = \int\limits_0^2 {\left| {\left( {5x - {x^2}} \right) - \left( {{x^2} - x} \right)} \right|dx} = \int\limits_0^2 {\left| {6x - 2{x^2}} \right|dx} = 2\int\limits_0^2 {\left| {{x^2} - 3x} \right|dx} \)
Ta có \({x^2} - 3x = 0 \Leftrightarrow x = 0\) hoặc \(x = 3\)
Do đó \(S = \left| {\int\limits_0^2 {\left( {{x^2} - 3x} \right)dx} } \right| = \left| {\left. {\left( {\frac{{{x^3}}}{3} - 3\frac{{{x^2}}}{2}} \right)} \right|_0^2} \right| = \left| { - \frac{{10}}{3}} \right| = \frac{{10}}{3}\)
(Trả lời bởi Nguyễn Quốc Đạt)
Mặt cắt của một cửa hầm có dạng là hình phẳng giới hạn bởi một parabol và đường thẳng nằm ngang như Hình 7. Tính diện tích của cửa hầm.
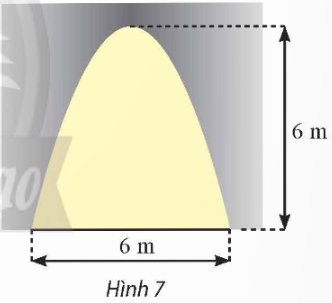
Thảo luận (1)Hướng dẫn giảiTa ghép mặt cắt của cửa hầm vào mặt phẳng \(Oxy\) như hình vẽ dưới đây. Diện tích của cửa hầm chính là diện tích hình phẳng giới hạn bởi parabol \(y = f\left( x \right) = a{x^2} + bx + c\), trục hoành và hai đường thẳng \(x = 0\), \(x = 6\).
Ta nhận thấy rằng parabol đi qua các điểm có toạ độ \(\left( {0;0} \right)\), \(\left( {6;0} \right)\) và \(\left( {3;6} \right)\) (trục đối xứng của parabol đi qua đỉnh), do đó ta có hệ phương trình:
\(\left\{ {\begin{array}{*{20}{c}}{a{{.0}^2} + b.0 + c = 0}\\{a{{.6}^2} + b.6 + c = 0}\\{a{{.3}^2} + b.3 + c = 6}\end{array} \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{c = 0}\\{36a + 6b + c = 0}\\{9a + 3b + c = 6}\end{array}} \right. \Leftrightarrow \left\{ {\begin{array}{*{20}{c}}{a = - \frac{2}{3}}\\{b = 4}\\{c = 0}\end{array}} \right.} \right.\)
Vậy phương trình của parabol là \(y = - \frac{2}{3}{x^2} + 4x\).
Ta thấy rằng với \(x \in \left[ {0;6} \right]\) thì parabol nằm trên trục hoành. Do đó, diện tích của cửa hầm, cũng chính là diện tích hình phẳng giới hạn bởi parabol \(y = - \frac{2}{3}{x^2} + 4x\), trục hoành và các đường thẳng \(x = 0\), \(x = 6\) là:
\(S = \int\limits_0^6 {\left| { - \frac{2}{3}{x^2} + 4x} \right|dx} = \int\limits_0^6 {\left( { - \frac{2}{3}{x^2} + 4x} \right)dx} = \left. {\left( {\frac{{ - 2}}{9}{x^3} + 2{x^2}} \right)} \right|_0^6 = 24\)
Vậy diện tích của cửa hầm là 24 \({{\rm{m}}^2}\).
(Trả lời bởi Nguyễn Quốc Đạt)
Trong không gian, cho hình chóp O.ABCD có đáy là hình vuông cạnh a, OA \(\perp\) (ABCD), OA = h. Đặt trục số Ox như Hình 8. Một mặt phẳng vuông góc với trục Ox tại điểm có hoành độ x (0 < x ≤ h), cắt hình chóp O.ABCD theo mặt cắt là hình vuông A'B'C'D'. Kí hiệu S(x) là diện tích của hình vuông A'B'C'D'.
a) Tính S(x) theo a, h và x.
b) Tính \(\int\limits^h_0S\left(x\right)dx\) và so sánh với thể tích của khối chóp O.ABCD.
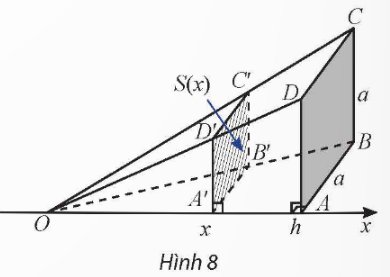
Thảo luận (1)Hướng dẫn giảia) Do \(A'B'C'D'\) là hình vuông, nên \(S\left( x \right) = A'D{'^2}\)
Tam giác \(OAD\) có \(AD\parallel A'D'\) nên \(\frac{{OA'}}{{OA}} = \frac{{A'D'}}{{AD}} \Rightarrow A'D' = \frac{{OA'.AD}}{{OA}} = \frac{{x.a}}{h}\)
Suy ra \(S\left( x \right) = A'D{'^2} = {\left( {\frac{{x.a}}{h}} \right)^2} = \frac{{{a^2}}}{{{h^2}}}{x^2}\)
b) Ta có: \(\int\limits_0^h {S\left( x \right)dx} = \frac{{{a^2}}}{{{h^2}}}\int\limits_0^h {{x^2}dx} = \frac{{{a^2}}}{{{h^2}}}\left. {\left( {\frac{{{x^3}}}{3}} \right)} \right|_0^h = \frac{{{a^2}}}{{{h^2}}}.\frac{{{h^3}}}{3} = \frac{{{a^2}h}}{3}\)
Thể tích khối chóp \(O.ABCD\) là \({V_{O.ABCD}} = \frac{1}{3}.{a^2}.h = \frac{{{a^2}h}}{3}\)
Như vậy \({V_{O.ABCD}} = \int\limits_0^h {S\left( x \right)dx} \)
(Trả lời bởi Nguyễn Quốc Đạt)
Một bình chứa nước có hình dạng như Hình 11. Biết rằng khi nước trong bình có chiều cao x (dm) (0 ≤ x ≤ 4) thì mặt nước là hình vuông có cạnh \(\sqrt{2+\dfrac{x^2}{4}}\) (dm). Tính dung tích của bình.
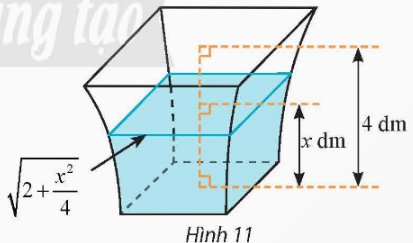
Thảo luận (1)Hướng dẫn giảiChọn trục \(Ox\) vuông góc với mặt đáy của bình sao cho đáy nhỏ, đáy to của bình vuông góc với \(Ox\) lần lượt tại \(x = 0\) và \(x = 4\)
Diện tích mặt nước ở chiều cao \(x\) là \(S\left( x \right) = {\left( {\sqrt {2 + \frac{{{x^2}}}{4}} } \right)^2} = 2 + \frac{{{x^2}}}{4}\)
Dung tích của bình là \(V = \int\limits_0^4 {S\left( x \right)dx} = \int\limits_0^4 {\left( {2 + \frac{{{x^2}}}{4}} \right)dx} = \left. {\left( {2x + \frac{{{x^3}}}{{12}}} \right)} \right|_0^4 = \frac{{40}}{3}\)
(Trả lời bởi Nguyễn Quốc Đạt)