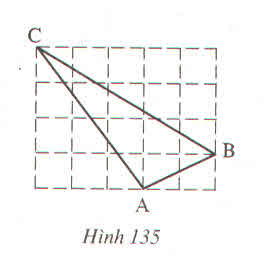
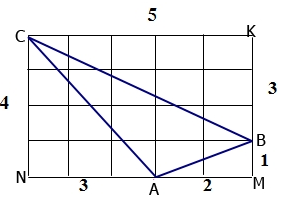
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34
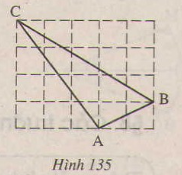
Giải:
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2=AN2+NC2
=9+16=52
nên AC=5
BC2=BK2+KC2
= 32+52=9+25=34
BC= √34
Áp dụng định lí Pi-ta-go trong ΔAMB ta có:
AB2 = AM2 + MB2 = 22 + 12 = 5
=> AB = √5
Áp dụng định lí Pi-ta-go trong ΔANC ta có:
AC2 = AN2 + NC2 = 32 + 42 = 25
=> AC = 5
Áp dụng định lí Pi-ta-go trong ΔBKC ta có:
BC2 = BK2 + KC2 = 32 + 52 = 34
=> BC = √34
Ta có: AB2=AM2+MB2
=22+12=5
Nên AB= √5
AC2 = AN2+NC2
= 9+16 = 25
nên AC = 5
BC2 = BK2 + KC2
= 32 + 52= 9+25=34
BC = √34
Áp dụng định lí Pi-ta-go trong ΔAMB vuông tại M ta có:
AB2 = AM2 + MB2 = 22 + 12 = 5
⇒ AB = √5
Áp dụng định lí Pi-ta-go trong ΔANC vuông tại N ta có:
AC2 = AN2 + NC2 = 32 + 42 = 25
⇒ AC = 5
Áp dụng định lí Pi-ta-go trong ΔBKC vuông tại K ta có:
BC2 = BK2 + KC2 = 32 + 52 = 34
⇒ BC = √34