Chương 4: GIỚI HẠN
Các câu hỏi tương tự
Bài 8: cho hàm số f(x) = (x ^ 2 + x - 6)/(x - 2); 2x + 1 khi x=2 khi x=2 Xét tính liên tục của hàm số tại x = 2
Tìm a để các hàm số sau liên tục tại x0
\(f\left(x\right)=\left\{{}\begin{matrix}\dfrac{\sqrt{1-x}+\sqrt{1+x}}{x}khix< 0\\a+\dfrac{4-x}{x+2}khi\ge0\end{matrix}\right.\)tại x0 = 0
Cho hàm số \(\left\{{}\begin{matrix}\dfrac{\sqrt[3]{ax+b}-1}{x}\Leftrightarrow\left(x\ne0\right)\\a+b+c-2=0\left(x=0\right)\end{matrix}\right.\) liên tục tại điểm x=0 ( Trong đó a,b,c>0).Tìm giá trị lớn nhất của biểu thức P=a.b.cA.3 B.3/4 C.1/3 ...
Xem chi tiết
Tìm giới hạn của hàm số sau:
\(\lim\limits_{x\rightarrow2}\dfrac{x^2-3x+2}{x-2}\)
Tìm giới hạn của hàm số sau:
\(\lim\limits_{x\rightarrow a}\dfrac{x^4-a^4}{x^2-a^2}\)
giá trị của a để hàm số
f(x)=\(\left\{{}\begin{matrix}x+2ax< 0\\x^2+x+1,x\ge0\end{matrix}\right.\)
liên tục tại x=0
Hàm số nào sau đây liên tục trên toàn bộ tập số thực R
A/ f(X)=√x2+2x+1
B/ g(x)= 4x^2-5x^2+1
C/ h(x)= x-1/ x+1
D/ y= tanx
Tìm giới hạn của hàm số sau:
\(\lim\limits_{x\rightarrow1}\dfrac{\sqrt{2x+7}-3}{x-1}\)
Cho hàm số \(f\left(x\right)=2x-3\) và dãy số \(\left(x_n\right)\) , lim \(x_n=1\) . Tính \(limf\left(x_n\right)\)

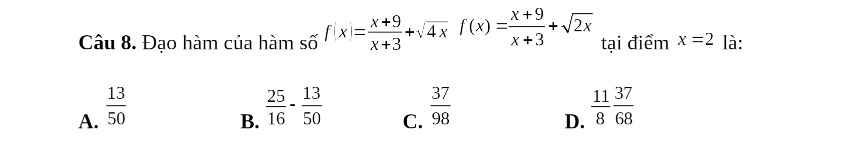 x= 2 :}
x= 2 :}







