Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Chương 1: VECTƠ
Các câu hỏi tương tự
cho tam giác ABC có trọng tâm G . Gọi P,Q là hai điểm thỏa mãn :
\(3\overrightarrow{PA}+2\overrightarrow{PB}=\overrightarrow{0},\overrightarrow{QA}-2\overrightarrow{QC}=\overrightarrow{0}\)
chứng minh 3 điểm : G,Q,P thẳng hàng
Cho ∆ABC với vecto MB= –2 vecto MA, vecto NA+ vecto NC= vecto 0. Gọi k là trung điểm MN.
a) Chứng minh 2vecto AB + 3vecto AC= 12 vecto AK.
b) Với P là điểm tùy ý, gọi Q là điểm thỏa vecto PQ= vecto PA +2vecto PB + vecto PC. Chứng minh đường thẳng PQ luôn đi qua điểm cố định.
🆘🆘🆘GIẢI GIÚP MÌNH VỚI 🆘🆘🆘
Cho ∆ABC với vecto MB= –2 vecto MA, vecto NA+ vecto NC= vecto 0. Gọi k là trung điểm MN.
a) Chứng minh 2vecto AB + 3vecto AC= 12 vecto AK.
b) Với P là điểm tùy ý, gọi Q là điểm thỏa vecto PQ= vecto PA +2vecto PB + vecto PC. Chứng minh đường thẳng PQ luôn đi qua điểm cố định.
cho ngũ giác ABCDE. xác định vị trí điểm M, N, P sao cho:
a. overrightarrow{2MB}-3overrightarrow{MC}overrightarrow{0}
b. overrightarrow{2NA}+2overrightarrow{NB}-overrightarrow{NC}overrightarrow{0}
c. 3overrightarrow{PA}+overrightarrow{PB}+overrightarrow{PC}+overrightarrow{PD}overrightarrow{0}
d. overrightarrow{QA}+overrightarrow{QB}+overrightarrow{QC}+3left(overrightarrow{OD}+overrightarrow{QE}right)overrightarrow{0}
Đọc tiếp
cho ngũ giác ABCDE. xác định vị trí điểm M, N, P sao cho:
a. \(\overrightarrow{2MB}-3\overrightarrow{MC}=\overrightarrow{0}\)
b. \(\overrightarrow{2NA}+2\overrightarrow{NB}-\overrightarrow{NC}=\overrightarrow{0}\)
c. \(3\overrightarrow{PA}+\overrightarrow{PB}+\overrightarrow{PC}+\overrightarrow{PD}=\overrightarrow{0}\)
d. \(\overrightarrow{QA}+\overrightarrow{QB}+\overrightarrow{QC}+3\left(\overrightarrow{OD}+\overrightarrow{QE}\right)=\overrightarrow{0}\)
Đề là chứng minh M N và P thẳng hàng nha cái chỗ khó nhìn là thoả mãn
Giúp mik với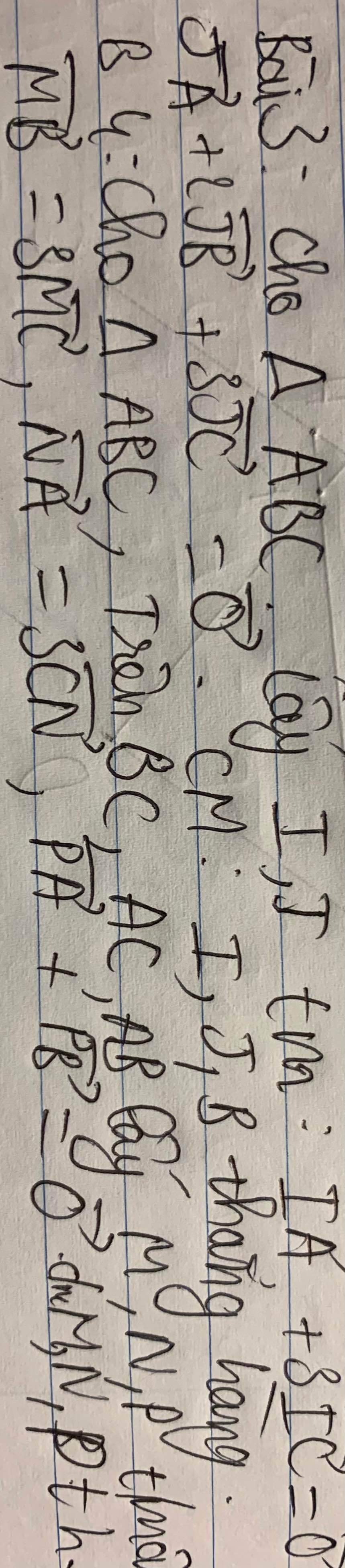
Cho tam giác ABC. Trên các đường thẳng BC, AC, AB lần lượt lấy các điểm M, N, P sao cho overrightarrow{NA}3.overrightarrow{CN}; overrightarrow{MB}3.overrightarrow{MC}; overrightarrow{PA}+overrightarrow{PB}overrightarrow{0} a) Tính overrightarrow{PM}; overrightarrow{PN} theo overrightarrow{AB};overrightarrow{AC} b) Chứng minh: M, N, P thẳng hàng
Đọc tiếp
Cho tam giác ABC. Trên các đường thẳng BC, AC, AB lần lượt lấy các điểm M, N, P sao cho \(\overrightarrow{NA}=3.\overrightarrow{CN}\); \(\overrightarrow{MB}=3.\overrightarrow{MC}\); \(\overrightarrow{PA}+\overrightarrow{PB}=\overrightarrow{0}\)
a) Tính \(\overrightarrow{PM}\); \(\overrightarrow{PN}\) theo \(\overrightarrow{AB};\overrightarrow{AC}\)
b) Chứng minh: M, N, P thẳng hàng
Cho đoạn AB có P,Q di động thoả mãn vector PQ=2PA+3PB. CMR đường thẳng PQ luôn đi qua một điểm cố định
1.Cho tam giác ABC, gọi G là trọng tâm tam giác a.Gọi H là điểm đối xứng với G qua B. CMRvectơ HA - 5vectơ HB + vectơ HC vectơ 0.b.Gọi I và J là 2 điểm thoả mãn vectơ IA 2vectơ IB , 3vectơ JA + 2vectơ JC vectơ 0 . CM 3 điểm I,J,G thẳng hàng .2.Cho tam giác đều ABC tâm O. M là điểm bất kì trong tam giác . Hạ MD,ME,MF lần lượt vuông góc với các cạnh BC,CA,AB.CMR vectơ MD + vectơ ME + vectơ MF 3/2 vectơ MO
Đọc tiếp
1.Cho tam giác ABC, gọi G là trọng tâm tam giác
a.Gọi H là điểm đối xứng với G qua B. CMR
vectơ HA - 5vectơ HB + vectơ HC = vectơ 0.
b.Gọi I và J là 2 điểm thoả mãn vectơ IA = 2vectơ IB , 3vectơ JA + 2vectơ JC = vectơ 0 . CM 3 điểm I,J,G thẳng hàng .
2.Cho tam giác đều ABC tâm O. M là điểm bất kì trong tam giác . Hạ MD,ME,MF lần lượt vuông góc với các cạnh BC,CA,AB.CMR vectơ MD + vectơ ME + vectơ MF = 3/2 vectơ MO
1.Cho tam giác ABC,K là trung điểm của AB. Điểm I thoả mãn \(\overrightarrow{IB}\)= 2\(\overrightarrow{IC}\)
a, Biểu diễn \(\overrightarrow{IK}\) theo 2 véc tơ \(\overrightarrow{AB}\) và \(\overrightarrow{AC}\)
b, J thuộc đoạn thẳng AC sao cho JA= 2JC . Chứng minh I,J,K thẳng hàng
làm họ mik vs








