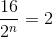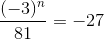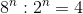a) \(\dfrac{16}{2^n}=2\Rightarrow2^n=\dfrac{16}{2}=8=2^3\)
\(\Rightarrow n=3\)
b) \(\dfrac{\left(-3\right)^n}{81}=-27\)
\(\Leftrightarrow\dfrac{\left(-3\right)^n}{3^4}=\left(-3\right)^3\)
\(\Leftrightarrow\left(-3\right)^n=-\left(3^4\cdot3^3\right)=\left(-3\right)^7\)
\(\Rightarrow n=7\)
c) \(8^n:2^n=4\)
\(\Leftrightarrow2^{3n}:2^n=2^2\)
\(\Leftrightarrow3n-n=2\)
\(\Leftrightarrow2n=2\Rightarrow n=1\)
a, \(\dfrac{16}{2^n}=2\Rightarrow2^n.2=16\Rightarrow2^{n+1}=2^4\Rightarrow n+1=4\Rightarrow n=3\). Vậy n=3.
b, \(\dfrac{\left(-3\right)^n}{81}=-27\Rightarrow\left(-3\right)^n=81.\left(-27\right)\Rightarrow\left(-3\right)^n=-2187\)
\(\Rightarrow\left(-3\right)^n=\left(-3\right)^7\Rightarrow n=7\)
Vậy n=7
c, \(8^n:2^n=4\Rightarrow\left(2^3\right)^n:2^n=2^2\Rightarrow2^{3n}:2^n=2^2\Rightarrow2^{2n}=2^2\Rightarrow2n=2\Rightarrow n=1\)
Vậy n=1.
a)
\(\dfrac{16}{2^n}=2\\ =>2.2^n=16\\ < =>2^n=\dfrac{16}{2}=8\\ Mà:2^3=8\\ =>2^3=2^n\\ =>n=3\)
b) \(\dfrac{\left(-3\right)^n}{81}=-27\\ < =>-27.81=\left(-3\right)^n\\ < =>\left(-3\right)^3.\left(-3\right)^4=\left(-3\right)^n\\ < =>\left(-3\right)^7=\left(-3\right)^n\\ =>n=7\)
c) \(8^n:2^n=4\\ < =>\left(8:2\right)^n=4\\ < =>4^n=4\\ Mà:4^1=4\\ =>4^n=4^1\\ =>n=1\)
a) \(\dfrac{16}{2^n}\) = 2
\(\Leftrightarrow\) 16 : \(2^n\) = 2
\(\Leftrightarrow\) \(2^n\) = 16 : 2
\(\Rightarrow\) \(2^n\) = 8
\(\Rightarrow\) \(n\) = 3
b) \(\dfrac{\left(-3\right)^n}{81}\) = \(-\)27
\(\Leftrightarrow\) \(\left(-3\right)^n\) : 81 = \(-27\)
\(\Leftrightarrow\) \(\left(-3\right)^n\) = \(-27\) . 81
\(\Rightarrow\) \(\left(-3\right)^n\) = \(-2187\)
\(\)\(\Rightarrow\) \(n\) = 7
c) \(8^n\) : \(2^n\) = 4
\(\Leftrightarrow\) \(4^{n^2}\) = 4
\(\Rightarrow\) n = 1
a) \(\dfrac{16}{2^n}=2\)
\(\Rightarrow2.2^n=16\)
\(\Rightarrow4^n=4^2\)
=> n = 2
b) \(\dfrac{\left(-3\right)^n}{81}=-27\)
\(\Rightarrow\dfrac{\left(-3\right)^n}{\left(-3\right)^4}=\left(-3\right)^3\)
\(\Rightarrow\left(-3\right)^n=\left(-3\right)^3.\left(-3\right)^4\)
\(\Rightarrow\left(-3\right)^n=\left(-3\right)^{3+4}\)
\(\Rightarrow\left(-3\right)^n=\left(-3\right)^7\)
=> n = 7
c) \(8^n:2^n=4\)
\(\Rightarrow\left(8:2\right)^n=4\)
\(\Rightarrow4^n=4\)
=> n = 1