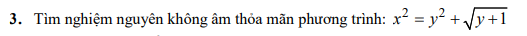Phương trình đã cho tương đương
\(y^3=x^3+4x^2+x+2\)
Ta có \(x^3+4x^2+x+2=x^3+15x^2+75x+125-11x^2-74x-123\)
\(=\left(x+5\right)^3-\left(x+3\right)\left(11x+41\right)\)
Do \(\left(x+3\right)\left(11x+41\right)\ge0\) \(\forall x\in Z\) (khoảng giá trị âm rơi vào giữa \(-3\) và \(-4\), không tồn tại ở các giá trị \(x\) nguyên)
\(\Rightarrow\left(x+5\right)^3-\left(x+3\right)\left(11x+41\right)\le\left(x+5\right)^3\) (1)
\(\Rightarrow y^3\le\left(x+5\right)^3\)
Lại có \(x^3+4x^2+x+2=x^3+3x^2+3x+1+x^2-2x+1\)
\(=\left(x+1\right)^3+\left(x-1\right)^2\ge\left(x+1\right)^3\) do \(\left(x-1\right)^2\ge0\) (2)
\(\Rightarrow y^3\ge\left(x+1\right)^3\)
\(\Rightarrow\left(x+1\right)^3\le y^3\le\left(x+5\right)^3\Rightarrow x+1\le y\le x+5\)
Ta xét các trường hợp:
TH1: \(y=x+1\Leftrightarrow\left\{{}\begin{matrix}x=1\\y=2\end{matrix}\right.\) (dấu "=" ở trường hợp 1, xảy ra khi \(x-1=0\))
TH2: \(y=x+2\)
\(\Rightarrow\left(x+2\right)^3=x^3+4x^2+x+2\Leftrightarrow2x^2+11x+6=0\Rightarrow\) ko có \(x\in Z\)
TH3: \(y=x+3\)
\(\Rightarrow\left(x+3\right)^3=x^3+4x^2+x+2\Leftrightarrow5x^2+26x+25=0\left(l\right)\)
TH4: \(y=x+4\)
\(\Rightarrow\left(x+4\right)^3=x^3+4x^2+x+2\Leftrightarrow8x^2+47x+62=0\)
\(\Rightarrow x=-2\Rightarrow y=2\)
TH5: \(y=x+5\Rightarrow\left\{{}\begin{matrix}x=-3\\y=2\end{matrix}\right.\) (dấu "=" xảy ra ở (1) khi \(x+3=0\))
Vậy các cặp nghiệm nguyên thỏa mãn là:
\(\left(x;y\right)=\left(1;2\right);\left(-2;2\right);\left(-3;2\right)\)