Bài 3: Trường hợp bằng nhau thứ nhất của tam giác canh - cạnh - cạnh (c.c.c)
Các câu hỏi tương tự
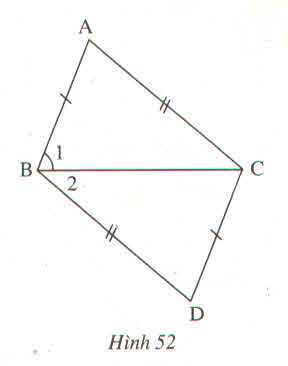
tìm chỗ sai trong bài làm sau đây của một học sinh (h.52) tam giác ABC = tam giác DBC (c.c.c) => B1 = B2 (cặp góc tương ứng) => BC là tia phân giác của góc ABD
Xét bài toán : Delta AMB và Delta ANB có MA MB, NA NB (h.71)
Chứng minh rằng : widehat{AMN}widehat{BMN}
1) Hãy ghi giả thiết và kết luận của bài toán
2) Hãy sắp xếp bốn câu sau đây một cách hợp lí để giải bài toàn trên
a) Do đó Delta AMNDelta BMN (c.c.c)
b) MN : cạnh chung
MA MB (giả thiết)
NA NB (giả thiết)
c) Suy ra widehat{AMN}widehat{BMN} (hai góc tương ứng)
a) Delta AMNDelta BMN có :
Đọc tiếp
Xét bài toán : " \(\Delta AMB\) và \(\Delta ANB\) có MA = MB, NA = NB (h.71)
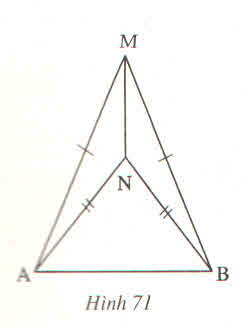
Chứng minh rằng : \(\widehat{AMN}=\widehat{BMN}\)
1) Hãy ghi giả thiết và kết luận của bài toán
2) Hãy sắp xếp bốn câu sau đây một cách hợp lí để giải bài toàn trên
a) Do đó \(\Delta AMN=\Delta BMN\) (c.c.c)
b) MN : cạnh chung
MA = MB (giả thiết)
NA = NB (giả thiết)
c) Suy ra \(\widehat{AMN}=\widehat{BMN}\) (hai góc tương ứng)
a) \(\Delta AMN=\Delta BMN\) có :
1, Cho Delta ABC biết widehat{A}widehat{B}widehat{C}. Tính số đo của mỗi góc2, Cho Delta ABC biết widehat{A} 70 độ; widehat{B}-widehat{C}10 độ. Tính widehat{B}; widehat{C}
Đọc tiếp
1, Cho \(\Delta ABC\) biết \(\widehat{A}\)=\(\widehat{B}\)=\(\widehat{C}\). Tính số đo của mỗi góc
2, Cho \(\Delta ABC\) biết \(\widehat{A}\)= 70 độ; \(\widehat{B}\)-\(\widehat{C}\)=10 độ. Tính \(\widehat{B}\); \(\widehat{C}\)
Cho \(\Delta ABC\) có \(\widehat{A}=77\) độ (AB < AC). Trên AC lấy điểm D sao cho thỏa mãn điều kiện \(\widehat{DBC}=\widehat{C}\); \(\widehat{ADB}=\widehat{ABD}\). Tính số đo của góc B và góc C của tam giác ABC.
1.
a) Vẽ vào vở ΔABC, biết AB 2,5 cm ; AC 3,5 cm ; BC 7 cm .
b) Vẽ vào vở ΔEFG , có EF FG GE 3 cm . Sau đó đo ba góc của tam giác EFG rồi cho biết số đo của mỗi góc .
c) Sắp xếp lại trình tự các bước chứng minh bài toán sau
Bài toán : ΔAMB và ΔANB có MA MB , NA NB ( h.69 ) . Chứng minh rằng ∠AMN ∠ BMN .
Các bước chứng minh :
i) Do đó ΔAMN ΔBMN ( c.c.c )
ii) MN : cạnh chung ;
MA MB ( giả thiết )
NA NB ( giả thiết )
iii) Suy ra ∠AMN ∠BMN (hai góc tương ứng )...
Đọc tiếp
1.
a) Vẽ vào vở ΔABC, biết AB = 2,5 cm ; AC = 3,5 cm ; BC = 7 cm .
b) Vẽ vào vở ΔEFG , có EF = FG = GE = 3 cm . Sau đó đo ba góc của tam giác EFG rồi cho biết số đo của mỗi góc .
c) Sắp xếp lại trình tự các bước chứng minh bài toán sau
Bài toán : " ΔAMB và ΔANB có MA = MB , NA = NB ( h.69 ) . Chứng minh rằng ∠AMN = ∠ BMN " .
Các bước chứng minh :
i) Do đó ΔAMN = ΔBMN ( c.c.c )
ii) MN : cạnh chung ;
MA = MB ( giả thiết )
NA = NB ( giả thiết )
iii) Suy ra ∠AMN = ∠BMN (hai góc tương ứng )
iv) ΔAMN và ΔBMN có :
2 . a) Ví dụ
Cho hình 70 , chứng minh DE là tia phân giác của ∠ADB .
Xét ΔADE và ΔBDE , từ hình vẽ ta có :
AD = BD ; AE = BE ; DE là cạnh chung.
Do đó ΔADE = ΔBDE ( c.c.c ) , suy ra ∠ADE = ∠BDE ( hai góc tương ứng ) .
b) Em hãy giải bài toán sau và viết vào vở như ví dụ trên .
Bài toán : Cho đoạn thẳng AB = 5 cm . Vẽ đường tròn tâm A bán kính 3 cm và đường tròn tâm B bán kính 4,5 cm , chúng cắt nhau ở C và D . Chứng minh rằng AB là tia phân giác của góc CAD .
Cho hình bs.1. Điền vào chỗ trống :
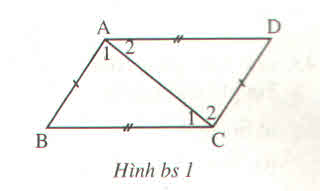
\(\widehat{A}_1=......\)
\(\widehat{A}_2=......\)
\(\widehat{B}=......\)
Cho tam giác ABC,góc A =90độ. Trên BC lấy E sao cho BE=BA. Tia phân giác của góc B cắt AC ở D chứng minh rằng:
a) tam giác ABD= tam giác EBD
b) tính số đo góc BED
c) BD vuông góc AE
Cho góc nhọn xOy. Trên Ox, Oy lấy tương ứng 2 điểm A và B sao cho OA = OB. Vẽ đường tròn tâm A và tâm B có cùng bán kính sao cho chúng cắt nhau tại 2 điểm M và N nằm trong \(\widehat{xOy}\). CMR:
a) \(\Delta OMA=\Delta OMB\) và \(\Delta ONA=\Delta ONB\)
b) 3 điểm O, M, N thẳng hàng
a) Vẽ tam giác ABC có BC = 2cm, AB = AC = 3cm
b) Gọi E là trung điểm của cạnh BC của tam giác ABC trong câu a). Chứng minh rằng AE là tia phân giác của góc BAC ?