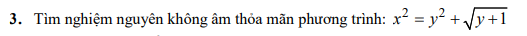Question

Tìm cặp số nguyên (x; y) thoả mãn phương trình: \(6x^2+5y^2=74\)

Answer 1

Vi 6x²≥0 , 5y²≥0 => 5y²≤74

=> y²≤\(\dfrac{74}{5}\)

Do y nguyen nen y va y²≤\(\dfrac{74}{5}\)

nen y co the nhan cac gtri : 0,1,2,3

Voi y=0 thi 6x²=74 => x²=\(\dfrac{74}{6}\)

=> x=\(\pm\dfrac{\sqrt{74}}{\sqrt{6}}\left(KTM\right)\)

Voi y=1 thi: 6x²=69 => x=\(\pm\dfrac{\sqrt{69}}{\sqrt{6}}\left(KTM\right)\)

Voi y=2 thi 6x²=54 => x=\(\pm3\left(TM\right)\)

Voi y=3 thi 6x²=29 => x=\(\pm\dfrac{\sqrt{29}}{\sqrt{6}}\)