Toi không thấy hđt nào ở đây cả chỉ tách thành tổng,hiệu bình phương thoi
`a^2+2sqrta+8`
`=a^2-2a+1+2a+2sqrta+7`
`=(a-1)^2+2(a+sqrta+1/4)-1/2+7`
`=(a-1)^2+(sqrta+1/2)^2+13/2`.
Toi không thấy hđt nào ở đây cả chỉ tách thành tổng,hiệu bình phương thoi
`a^2+2sqrta+8`
`=a^2-2a+1+2a+2sqrta+7`
`=(a-1)^2+2(a+sqrta+1/4)-1/2+7`
`=(a-1)^2+(sqrta+1/2)^2+13/2`.
cho biểu thức
A = \(\left(\dfrac{\sqrt{x}+2}{x+2\sqrt{x}+1}-\dfrac{\sqrt{x}-2}{x-1}\right):\dfrac{\sqrt{x}}{\sqrt{x}+1}\)
1. Rút gọn biểu thức A
2. Tìm tất cả các số nguyên x để biểu thức A có giá trị là số nguyên
Câu 1.
a) Chứng minh: (ac + bd)2 + (ad – bc)2 = (a2 + b2)(c2 + d2)
b) Chứng minh bất dẳng thức Bunhiacôpxki: (ac + bd)2 ≤ (a2 + b2)(c2 + d2)
Câu 2.
Cho x + y = 2. Tìm giá trị nhỏ nhất của biểu thức: S = x2 + y2.
cho a,b,b là các số dương và a2+b2+c2=1. Tìm GTNN của biểu thức:
P=\(\dfrac{bc}{a}\)+\(\dfrac{ac}{b}\)+\(\dfrac{ab}{c}\)
cho 2 biểu thức sau A=\(\dfrac{7}{\sqrt{x}+8}\) ;B =\(\dfrac{\sqrt{x}}{\sqrt{x}+3}-\dfrac{2\sqrt{x}}{9-x}\) A)tìm a vs x=6 B)cm B=\(\dfrac{\sqrt{x}+8}{\sqrt{x}+3}\) C)với A,B nói trên tìm x để P=AB có giá trị là số nguyên giúp mk bài này vs ạ mình cần trước lúc 5h chiều nay
1. trong hệ trục toạ độ Oxy, biết đường thẳng y = ax - 1 đi qua điểm M (-1;1). tìm hệ số a
2. cho biểu thức P = \(\left(\dfrac{\sqrt{a}}{2}-\dfrac{1}{2\sqrt{a}}\right)\left(\dfrac{a-\sqrt{a}}{\sqrt{a}+1}-\dfrac{a+\sqrt{a}}{\sqrt{a}-1}\right)\)
a, rút gọn P
b, tìm a để \(P\ge-2\)
Chứng minh các đẳng thức sau

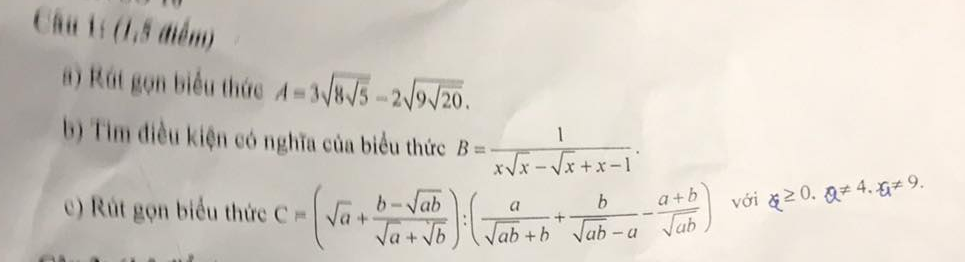
c1
a. rút gọn biểu thức
\(A=3\sqrt{8\sqrt{5}}-2\sqrt{9\sqrt{20}}\)
b. tìm đk có nghĩa của biểu thức
\(B=\dfrac{1}{x\sqrt{x}-\sqrt{x}+x-1}\)

Câu 1:
Cho phương trình: 2x2 + 5x - 8 = 0
a) Chứng tỏ phương trình luôn có hai nghiệm phân biệt x1, x2.
b) Không giải phương trình, hãy tính giá trị biểu thức: \(A=\dfrac{2}{x_1}+\dfrac{2}{x_2}.\)
Câu 2:
Cho biểu thức \(P=\dfrac{a+4\sqrt{a}+4}{\sqrt{a}+2}+\dfrac{4-a}{2-\sqrt{a}}\) (với a ≥ 0; a ≠ 4).
a) Rút gọn biểu thức P.
b) Tính \(\sqrt{P}\) tại a thỏa mãn điều kiện a2 - 7a + 12 = 0.
Câu 3:
a) Giải hệ phương trình: \(\left\{{}\begin{matrix}\dfrac{x}{y}=\dfrac{3}{2}\\3x-2y=5\end{matrix}\right.\)
b) Xác định hệ số a và b của hàm số y = ax + b biết đồ thị của nó là đường thẳng (d) song song với đường thẳng y = x + 2 và chắn trên hai trục tọa độ một tam giác có diện tích bằng 2.
Câu 4:
Cho đường tròn (O; R), đường kính AD. B là điểm chính giữa của nửa đường tròn, C là điểm trên cung AD không chứa điểm B (C khác A và D) sao cho tam giác ABC nhọn.
a) Chứng minh tam giác ABD vuông cân.
b) Kẻ AM ⊥ BC, BN ⊥ AC. Chứng minh tứ giác ABMN nội tiếp. Xác định tâm I đường tròn ngoại tiếp tứ giác ABMN.
c) Chứng minh điểm O thuộc đường tròn (I).
Cho các số thực a và b thỏa mãn a + b +ab = 8. Tính giá trị nhỏ nhất của biểu thức \(a^2+b^2\) .