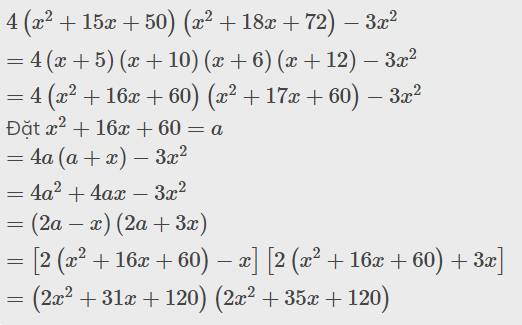\(4\left(x^2+15x+50\right)\left(x^2+18x+72\right)-3x^2\\ =4\left(x+5\right)\left(x+10\right)\left(x+6\right)\left(x+12\right)-3x^2\\ =4\left(x^2+16x+60\right)\left(x^2+17x+60\right)-3x^2\)
Đặt \(x^2+16x+60=a\)
\(=4a\left(a+x\right)-3x^2\\ =4a^2+4ax-3x^2\\ =\left(2a-x\right)\left(2a+3x\right)\\ =\left[2\left(x^2+16x+60\right)-x\right]\left[2\left(x^2+16x+60\right)+3x\right]\\ =\left(2x^2+31x+120\right)\left(2x^2+35x+120\right)\)
(x2+15x+50)(x2+18x+72)−3x2=4(x+5)(x+10)(x+6)(x+12)−3x2=4(x2+16x+60)(x2+17x+60)−3x24(�2+15�+50)(�2+18�+72)−3�2=4(�+5)(�+10)(�+6)(�+12)−3�2=4(�2+16�+60)(�2+17�+60)−3�2
Đặt x2+16x+60=a�2+16�+60=�
=4a(a+x)−3x2=4a2+4ax−3x2=(2a−x)(2a+3x)=[2(x2+16x+60)−x][2(x2+16x+60)+3x]=(2x2+31x+120)(2x2+35x+120)