Cấp số cộng có \(u_{10}=280\) ; \(d=20\)
\(\Rightarrow u_1=u_{10}-9d=100\)
Số ghế trong hội trường:
\(S_{10}=\frac{10\left(100+280\right)}{2}=1900\)
Chương 4: GIỚI HẠN
Các câu hỏi tương tự
Cho dãy số (Un) được xác định như sau: \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\). Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó
Cho dãy số (Un) được xác định như sau \(u_1=2023\), \(u_{n-1}=n^2.\left(u_{n-1}-u_n\right)\), với mọi n thuộc N*, \(n\ge2\) . Chứng minh rằng dãy số (Un) có giới hạn và tìm giới hạn đó
24 tháng 12 2023 lúc 10:59
Dãy số (Un) nào sau đây bị chặn:
A. Un=n-sin3n B.Un=\(\dfrac{n^2+1}{n}\) C.Un=\(\dfrac{1}{n\left(n+1\right)}\) D.Un=n.sin(3n-1)
Tìm giới hạn dãy số sau
\(lim\dfrac{\left(2n-1\right)\left(3n^2+2\right)^3}{-2n^5+4n^3-1}\)
\(lim\left(3.2^{n+1}-5.3^n+7n\right)\)
30 tháng 1 2021 lúc 17:20
Cho dãy \(\left(x_k\right)\) được xác định như sau: \(x_k=\dfrac{1}{2!}+\dfrac{2}{3!}+...+\dfrac{k}{\left(k+1\right)!}\)
Tìm \(limu_n\) với \(u_n=\sqrt[n]{x_1^n+x_2^n+...+x_{2011}^n}\).
Cho dãy un xác định bởi
\(\left\{{}\begin{matrix}x_1=3\\x_{n+1}=\dfrac{1}{2}x_n+2^{n-2}\end{matrix}\right.\) với n= 1,2,3,...
a) Tìm tất cả các số hạng là số nguyên dương trong dãy trên
b) Tìm số hạng tổng quát
Cho dãy số \(\left(u_n\right)\) xác định bởi \(\)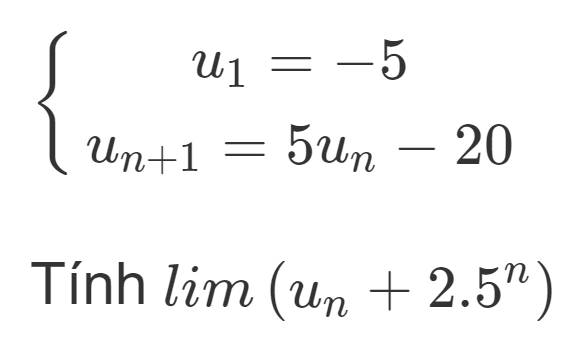
Cho hàm số \(f\left(x\right)=2x-3\) và dãy số \(\left(x_n\right)\) , lim \(x_n=1\) . Tính \(limf\left(x_n\right)\)
Cho hàm số \(f\left(x\right)=2x-3\) và dãy số \(\left(x_n\right)\) , lim \(x_n=1\) . Tính \(limf\left(x_n\right)\)