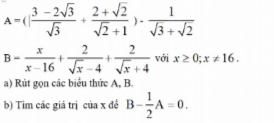`1a)A=4/(sqrt5-2)+\sqrt{(sqrt5-2)^2}-sqrt{125}`
`=(4(sqrt5+2))/(5-4)+sqrt5-2-5sqrt5`
`=4(sqrt5+2)-4sqrt5-2`
`=4sqrt5+8-4sqrt5-2`
`=6`
`B=(1/(sqrtx-2)+sqrtx/(x-4)).(3x-12)/(2sqrtx+2)`
`đk:x>=0,x ne 4`
`B((sqrtx+2+sqrtx)/(x-4)).(3(x-4))/(2sqrtx+2)`
`=(2sqrtx+2)/(x-4).(3(x-4))/(2sqrtx+2)`
`=3`
Câu 7:
Đặt A=\(\sqrt{a^2+abc}+\sqrt{b^2+abc}+\sqrt{c^2+abc}\)
\(=\sqrt{a}\sqrt{a+bc}+\sqrt{b}\sqrt{b+ac}+\sqrt{c}\sqrt{c+ab}\)\(\le\sqrt{\left(a+b+c\right)\left(a+b+c+ab+bc+ac\right)}\) (theo bđt bunhia)
\(\Rightarrow A\le\sqrt{1+ab+bc+ac}\)
mà \(ab+bc+ca\le\dfrac{\left(a+b+c\right)^2}{3}\) (bạn tự chứng minh được)
\(\Rightarrow A\le\sqrt{1+\dfrac{\left(a+b+c\right)^2}{3}}=\sqrt{1+\dfrac{1}{3}}=\dfrac{2\sqrt{3}}{3}\)
Áp dụng bđt cosi có:
\(1=a+b+c\ge\sqrt[3]{abc}\) \(\Leftrightarrow abc\le\dfrac{1}{27}\)
Có \(M=A+9\sqrt{abc}\le\dfrac{2\sqrt{3}}{3}+9\sqrt{\dfrac{1}{27}}=\dfrac{5\sqrt{3}}{3}\)
=> maxM\(=\dfrac{5\sqrt{3}}{3}\) \(\Leftrightarrow a=b=c=\dfrac{1}{3}\)