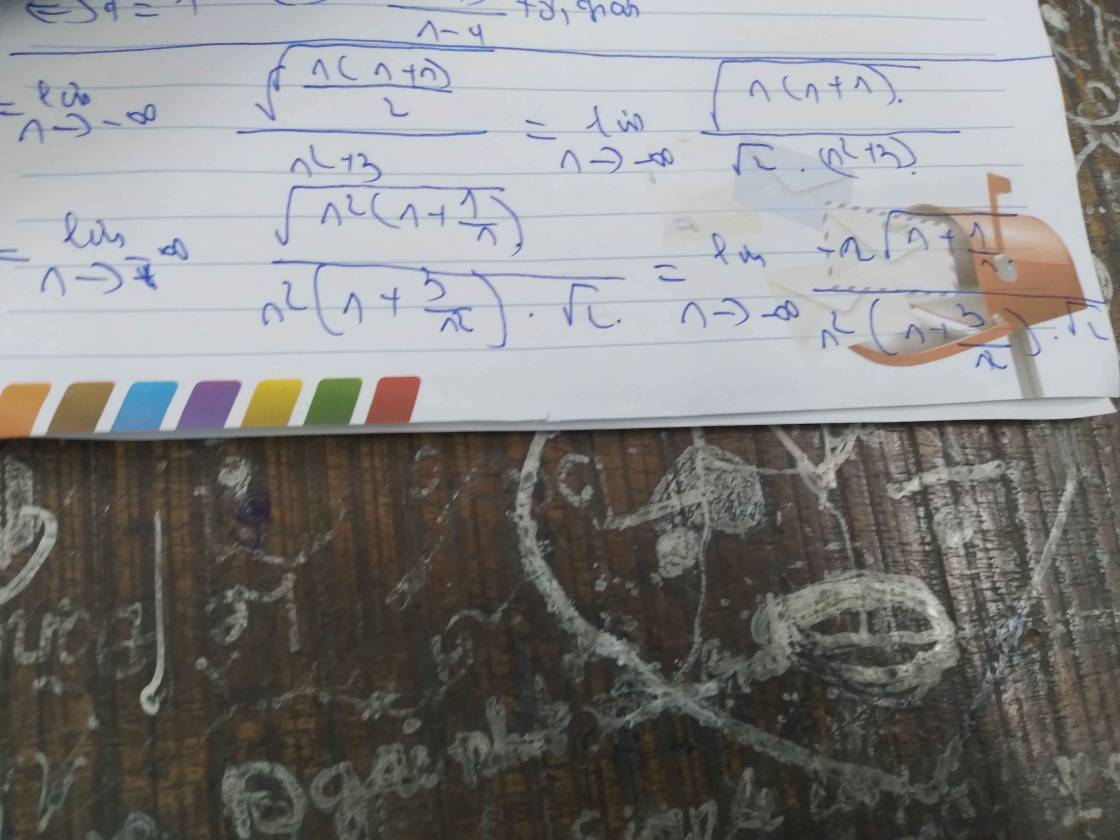\(1+2+...+n=\dfrac{n\left(n+1\right)}{2}=\dfrac{n^2+n}{2}\)
\(\Rightarrow\lim\limits\dfrac{\sqrt{1+2+...+n}}{n^2+3}=\lim\dfrac{\sqrt{\dfrac{n^2+n}{2}}}{n^2+3}=\lim\dfrac{\sqrt{\dfrac{1}{2}+\dfrac{1}{2n}}}{n+\dfrac{3}{n}}=\dfrac{\sqrt{\dfrac{1}{2}}}{+\infty}=0\)
`lim \sqrt{1+2+3+....+n}/[n^2+3]`
`=lim \sqrt{[n(n+1)]/2}/[n^2+3]`
`=lim \sqrt{n^2+n}/[\sqrt{2}n^2+3\sqrt{2}]`
`=lim \sqrt{1/[n^2]+1/[n^3]}/[\sqrt{2}+[3\sqrt{2}]/[n^2]]`
`=0/\sqrt{2}=0`