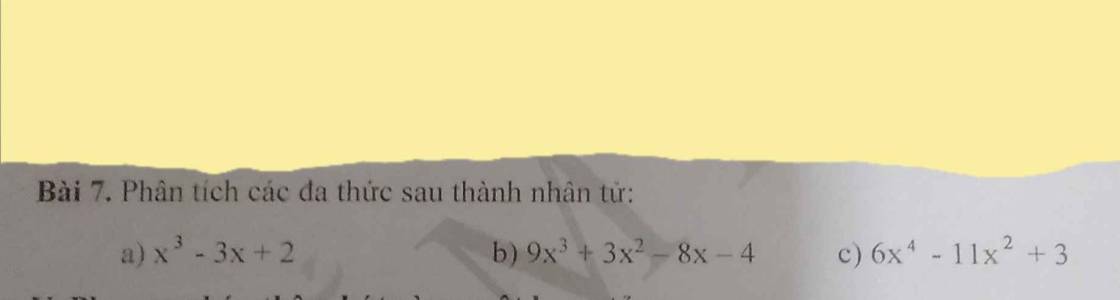a: Ta thấy khi x=1 thì \(x^3-3x+2=1^3-3\cdot1+2=1-3+2=0\)
=>x=1 là nghiệm của đa thức \(x^3-3x+2\)
Do đó, ta sẽ chia x^3-3x+2 cho x-1

Từ phép chia trên, ta sẽ có: \(x^3-3x+2=\left(x-1\right)\left(x^2-x-2\right)\)
mà ta lại có: \(x^2-x-2=x^2-2x+x-2=\left(x-2\right)\left(x+1\right)\)
nên \(x^3-3x+2=\left(x-1\right)\left(x-1\right)\left(x+2\right)=\left(x+2\right)\cdot\left(x-1\right)^2\)
b: Khi x=1 thì \(9x^3+3x^2-8x-4=9+3-8-4=0\)
=>x=1 là nghiệm của đa thức \(9x^3+3x^2-8x-4\)
Do đó, ta sẽ chia đa thức \(9x^3+3x^2-8x-4\) cho x-1

Từ phép chia trên, ta sẽ có: \(9x^3+3x^2-8x-4=\left(x-1\right)\left(9x^2+12x+4\right)\)
\(=\left(x-1\right)\left[\left(3x\right)^2+2\cdot3x\cdot2+2^2\right]\)
\(=\left(x-1\right)\left(3x+2\right)^2\)
c: Khi \(x^2=\dfrac{1}{3}\) thì \(6x^4-11x^2+3=6\left(x^2\right)^2-11x^2+3=6\cdot\left(\dfrac{1}{3}\right)^2-11\cdot\dfrac{1}{3}+3=6\cdot\dfrac{1}{9}+3-\dfrac{11}{3}=\dfrac{2}{3}+3-\dfrac{11}{3}=0\)
=>\(x^2=\dfrac{1}{3}\) là nghiệm của đa thức \(6x^4-11x^2+3\)
=>Ta sẽ chia đa thức \(6x^4-11x^2+3\) cho \(x^2-\dfrac{1}{3}\)
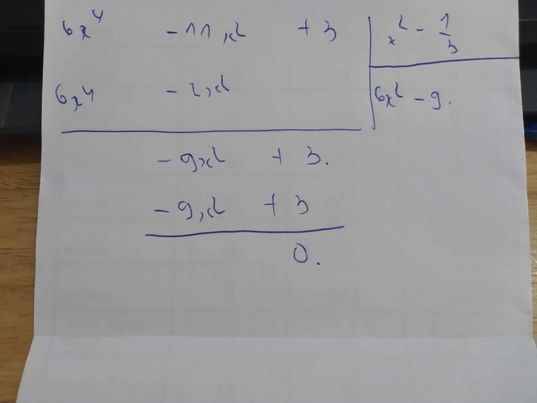
Từ phép chia trên, ta sẽ có:
\(6x^4-11x^2+3=\left(x^2-\dfrac{1}{3}\right)\left(6x^2-9\right)\)
\(=3\left(2x^2-3\right)\left(x^2-\dfrac{1}{3}\right)\)