Lời giải:
Đặt \(\left\{\begin{matrix} u=e^x\\ dv=2^xdx\end{matrix}\right.\Rightarrow \left\{\begin{matrix} du=e^xdx\\ v=\int2^xdx=\frac{2^x}{\ln 2}\end{matrix}\right.\)
Do đó \(I=\int 2^xe^xdx=\frac{2^xe^x}{\ln 2}-\frac{1}{\ln 2}\int 2^xe^xdx=\frac{2^xe^x}{\ln 2}-\frac{I}{\ln 2}\)
\(\Rightarrow \frac{I(\ln 2+1)}{\ln 2}=\frac{2^xe^x}{\ln 2}\)
\(\Rightarrow I=\frac{2^xe^x}{\ln 2+1}+c\)









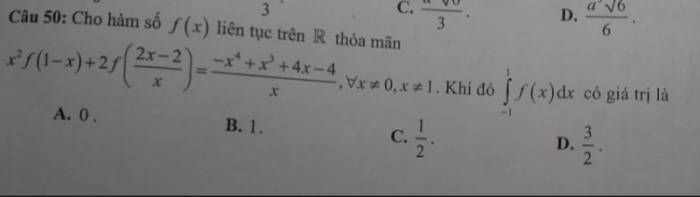 mọi người cho mình hỏi làm sao để xác định được cận của tích phân chạy từ 1 đến 2 ở bài này ?
mọi người cho mình hỏi làm sao để xác định được cận của tích phân chạy từ 1 đến 2 ở bài này ? 

