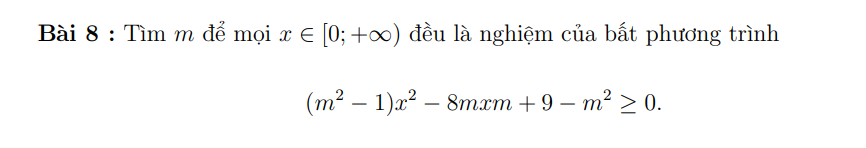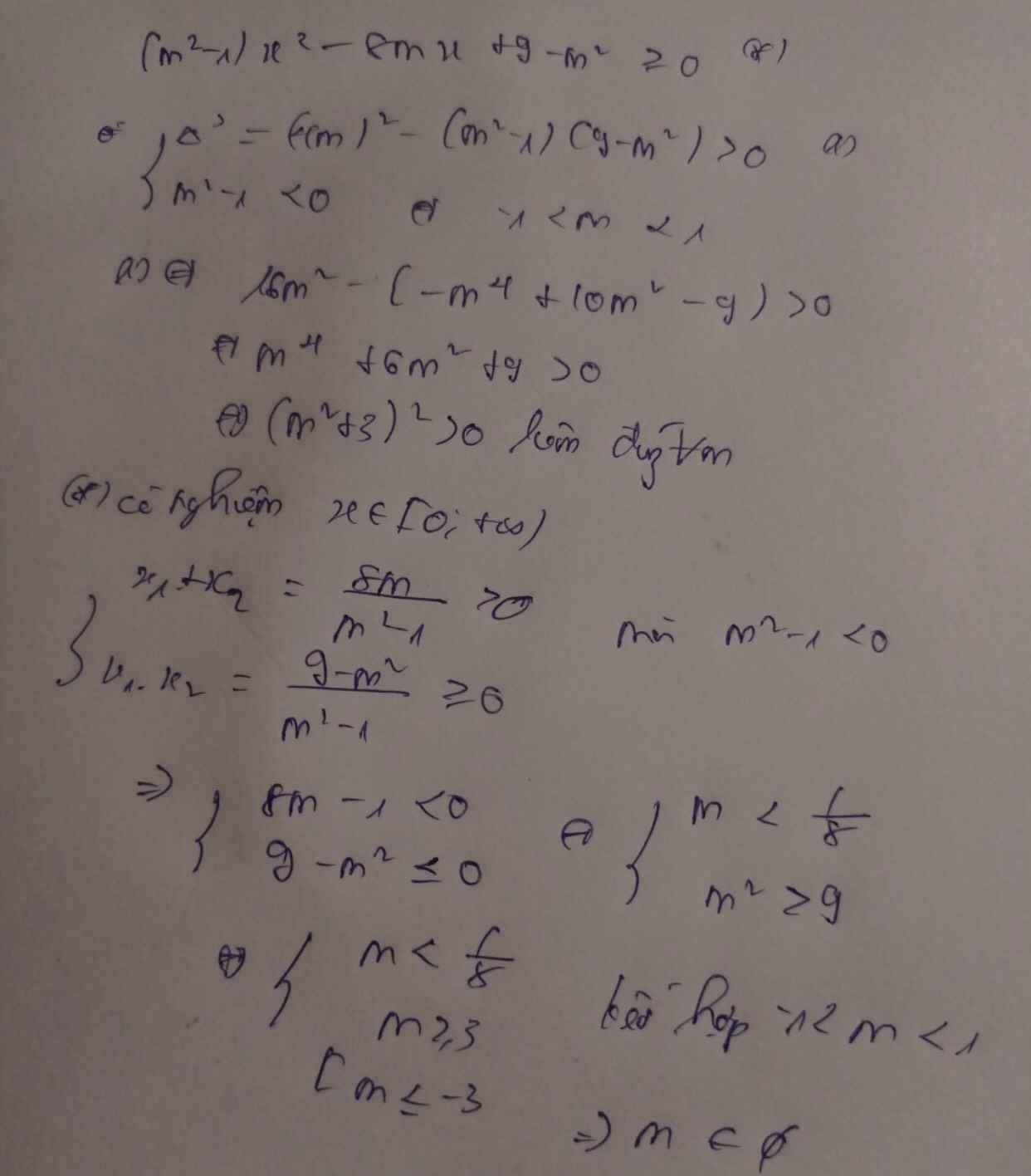\(f\left(x\right)=\left(m^2-1\right)x^2-8mx+9-m^2\ge0\)
\(TH1:m^2-1=0\Rightarrow m=\pm1\)
\(m=1\Rightarrow bpt\Leftrightarrow-8x+8\ge0\Leftrightarrow x\le1\left(loại\right)\)
\(m=-1\Rightarrow bpt\Leftrightarrow8x+8\ge0\Leftrightarrow x\ge-1\left(tm\right)\)
\(TH2:m^2-1>0\Leftrightarrow\left[{}\begin{matrix}m>1\\m< -1\end{matrix}\right.\)
\(\Delta=\left(8m\right)^2-4\left(9-m^2\right)\left(m^2-1\right)< 0\Leftrightarrow4x^4+24x^2+36=\left(2x^2\right)^2+2.2x^2.6+6^2=\left(2x^2+6\right)^2>0\left(\forall m\right)\)
\(\Rightarrow x1< x2\le0\Leftrightarrow\)\(\left\{{}\begin{matrix}x1x2\ge0\\x1+x2< 0\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}9-m^2\ge0\\8m< 0\end{matrix}\right.\)
\(\Leftrightarrow-3\le m< 0\Rightarrow-3\le m< -1\)
\(TH3:m^2-1< 0\Leftrightarrow-1< m< 1\)
\(f\left(x\right)\ge0\Leftrightarrow\Delta\le0\Leftrightarrow\left(2x^2+6\right)^2\le0\left(vô-lí\right)\)
\(\Rightarrow-3\le m\le-1\)