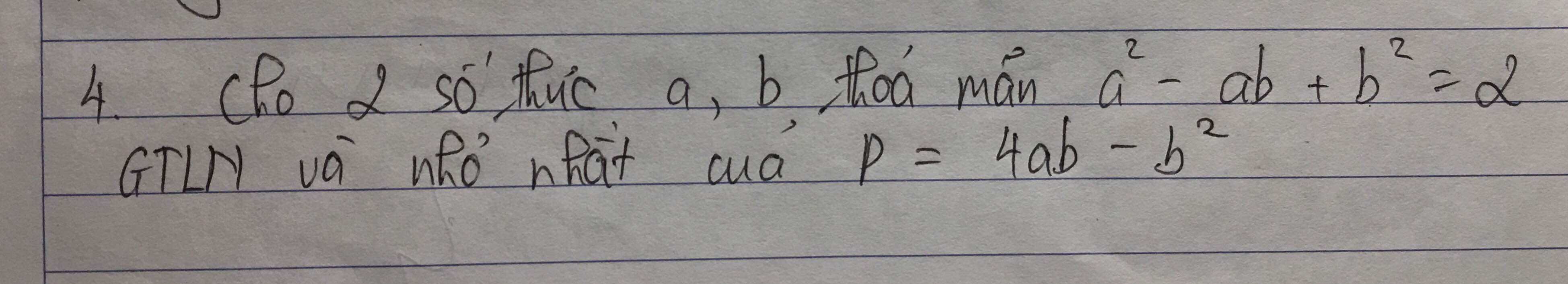Question

Help me huhuhuhuh

Answer 1

\(P=\dfrac{2\left(4ab-b^2\right)}{2}=\dfrac{8ab-2b^2}{a^2-ab+b^2}\)

Với \(b=0\Rightarrow P=0\)

Với \(b\ne0\Rightarrow P=\dfrac{8\left(\dfrac{a}{b}\right)-2}{\left(\dfrac{a}{b}\right)^2-\dfrac{a}{b}+1}\)

Đặt \(\dfrac{a}{b}=x\Rightarrow P=\dfrac{8x-2}{x^2-x+1}\Rightarrow Px^2-Px+P=8x-2\)

\(\Rightarrow Px^2-\left(P+8\right)x+P+2=0\)

\(\Delta=\left(P+8\right)^2-4P\left(P+2\right)\ge0\)

\(\Leftrightarrow-3P^2+8P+64\ge0\)

\(\Leftrightarrow\dfrac{4-4\sqrt{13}}{3}\le P\le\dfrac{4+4\sqrt{13}}{3}\)