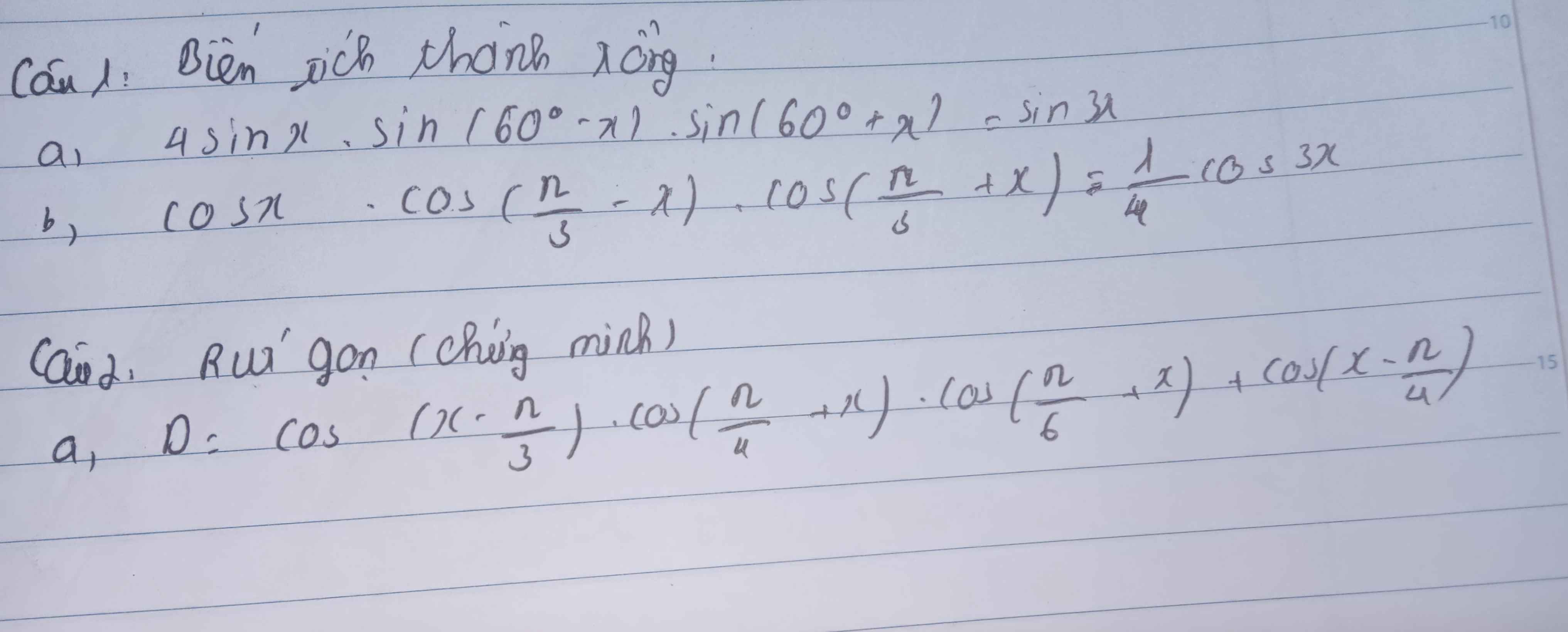1a.
\(4sinx.sin\left(60^0-x\right)sin\left(60^0+x\right)=2sinx\left(cos2x-cos120^0\right)\)
\(=2sinx.cos2x+sinx=sin3x-sinx+sinx=sin3x\)
b.
\(cosx.cos\left(\dfrac{\pi}{3}-x\right)cos\left(\dfrac{\pi}{3}+x\right)=\dfrac{1}{2}cosx\left(cos\dfrac{2\pi}{3}+cos2x\right)\)
\(=\dfrac{1}{2}cosx\left(-\dfrac{1}{2}+cos2x\right)=-\dfrac{1}{4}cosx+\dfrac{1}{2}cosx.cos2x\)
\(=-\dfrac{1}{4}cosx+\dfrac{1}{4}cos3x+\dfrac{1}{4}cosx=\dfrac{1}{4}cos3x\)