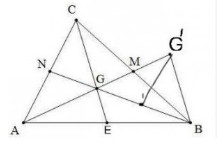
a) So sánh các cạnh của ∆BGG’ với các đường trung tuyến của ∆ABC BG cắt AC tại N
CG cắt AB tại E
G là trọng tâm của ∆ABC
=> GA = 
AM
Mà GA = GG’ ( G là trung điểm của AG ‘)
GG'= AM
Vì G là trọng tâm của ∆ABC => GB = BN
Mặt khác : GM = 
AG ( G là trọng tâm )
AG = GG '(gt)
GM = GG '
M là trung điểm GG’
Do đó ∆GMC = ∆G’MB vì :
GM = GM '
MB = MC
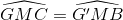
=> BG '= CG
mà CG = CE (G là trọng tâm ∆ABC)
=> BG = EC
Vậy mỗi cạnh của ∆BGG' bằng đường trung tuyến của ∆ABC
b) So sánh các đường trung tuyến của ∆BGG' với cạnh ∆ABC
ta có: BM là đường trung tuyến ∆BGG'
mà M là trung điểm của BC nên BM = BC
Vì IG = BG (I là trung điểm BG)
GN = BG ( G là trọng tâm)
=> IG = GN
Do đó ΔIGG '= ΔNGA (cgc) => IG' = AN => IG '=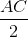 
- Gọi K là trung điểm BG => GK là trung tuyến ∆BGG'
Vì GE = GC (G là trọng tâm ∆ABC)
=> GE = BG
mà K là trung điểm BG' => KG' = EG
Vì ∆GMC = ∆G'BM (chứng minh trên)
=> 
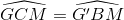(lại góc sole trong)
=> CE // BG' =>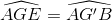 
(đồng vị)
Làm Độ ΔAGE = ΔGG'K (CGC) => AE = GK
mà AE = AB nên GK = AB
Vậy mỗi đường trung tuyến ∆BGG' bằng một nửa cạnh của tam giác ABC song song với nó
