Question

giúp tôi với mn

Answer 1

  

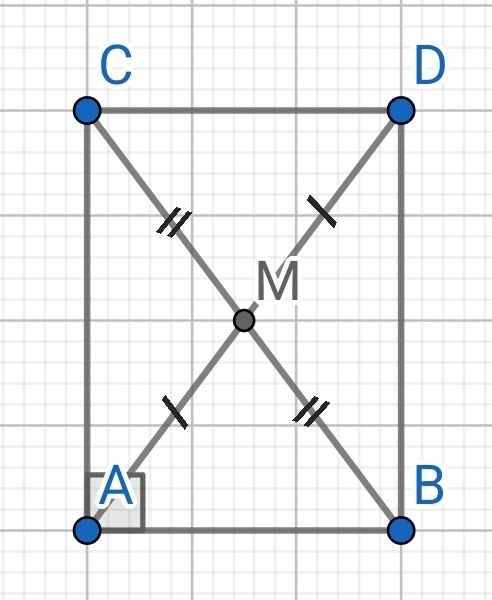
a) Do AM là đường trung tuyến của ∆ABC

⇒ M là trung điểm BC

Do MA = MD (gt)

⇒ M là trung điểm AD

Tứ giác ABDC có:

M là trung điểm BC (cmt)

M là trung điểm AD (cmt)

⇒ ABDC là hình bình hành

Mà ∠BAC = 90⁰ (gt)

⇒ ABDC là hình chữ nhật

b) ∆ABC vuông tại A

⇒ BC² = AB² + AC² (Pytago)

= 6² + 8²

= 100

⇒ BC = 10 (cm)

Do AM là đường trung tuyến ứng với cạnh huyền BC của ∆ABC

⇒ AM = BC : 2

= 10 : 2

= 5 (cm)

c) Nếu ∠B = 45⁰

⇒ C = 90⁰ - ∠B

= 90⁰ - 45⁰

= 45⁰

⇒ ∆ABC vuông cân tại A

⇒ AB = AC

Lại có ABDC là hình chữ nhật

⇒ ABDC là hình vuông