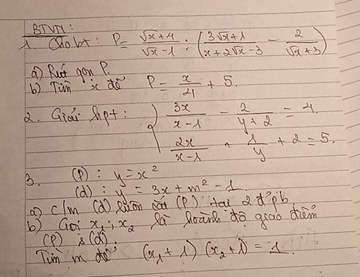a) Thay m = 5 vào phương trình, ta có:
\(x^2-10x+23=0\)
Xét \(\Delta=\left(-10\right)^2-4.1.23=8\)
=> \(\left\{{}\begin{matrix}x_1=\dfrac{10-\sqrt{8}}{2}=5-\sqrt{2}\\x_2=\dfrac{10+\sqrt{8}}{2}=5+\sqrt{2}\end{matrix}\right.\)
KL: Phương trình có nghiệm \(S\in\left\{5-\sqrt{2};5+\sqrt{2}\right\}\)
b) Xét \(\Delta=\left(-2m\right)^2-4.1.\left(m^2-m+3\right)\)
= \(4m^2-4m^2+4m-12=4m-12\)
Để phương trình có 2 nghiệm phân biệt <=> \(\Delta>0< =>m>3\)
Theo định lí Vi-ét, ta có: \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1.x_2=m^2-m+3\end{matrix}\right.\)
Để \(\dfrac{1}{x_1-3}+\dfrac{1}{x_2-3}=1\)
<=> \(\dfrac{x_2-3+x_1-3}{\left(x_1-3\right)\left(x_2-3\right)}-1=0\)
<=> \(x_1+x_2-6-\left(x_1-3\right)\left(x_2-3\right)=0\)
<=> \(x_1+x_2-6-x_1x_2+3x_1+3x_2-9=0\)
<=> \(4\left(x_1+x_2\right)-x_1x_2-15=0\)
<=> 8m - m2 + m -3 - 15 = 0
<=> m2 - 9m + 18 = 0
<=> (m-6)(m-3) = 0
<=> \(\left[{}\begin{matrix}m=6\left(c\right)\\m=3\left(l\right)\end{matrix}\right.\)
a) \(m=5\Rightarrow x^2-10x+23=0\)
\(\Delta-\left(-10\right)^2-4.23=8\Rightarrow\left[{}\begin{matrix}x=\dfrac{-b-\sqrt{\Delta}}{2a}=\dfrac{10-\sqrt{8}}{2}=5-\sqrt{2}\\x=\dfrac{-b+\sqrt{\Delta}}{2a}=\dfrac{10+\sqrt{8}}{2}=5+\sqrt{2}\end{matrix}\right.\)
b) \(\Delta'=m^2-m^2+m-3=m-3\)
Để pt có 2 nghiệm thì \(\Delta'\ge0\Rightarrow m\ge3\)
Áp dụng hệ thức Vi-ét \(\left\{{}\begin{matrix}x_1+x_2=2m\\x_1x_2=m^2-m+3\end{matrix}\right.\)
Ta có: \(\dfrac{1}{x_1-3}+\dfrac{1}{x_2-3}=1\left(x_1,x_2\ne0\right)\Rightarrow\dfrac{x_1+x_2-6}{\left(x_1-3\right)\left(x_2-3\right)}=1\)
\(\Rightarrow2m-6=x_1x_2-3\left(x_1+x_2\right)+9\Rightarrow2m-6=m^2-m+3-6m+9\)
\(\Rightarrow m^2-9m+18=0\Rightarrow\left(m-6\right)\left(m-3\right)=0\Rightarrow\left[{}\begin{matrix}m=6\\m=3\end{matrix}\right.\)
Thử lại \(\Rightarrow m=6\) (\(m=3\Rightarrow x_1=x_2=3\))