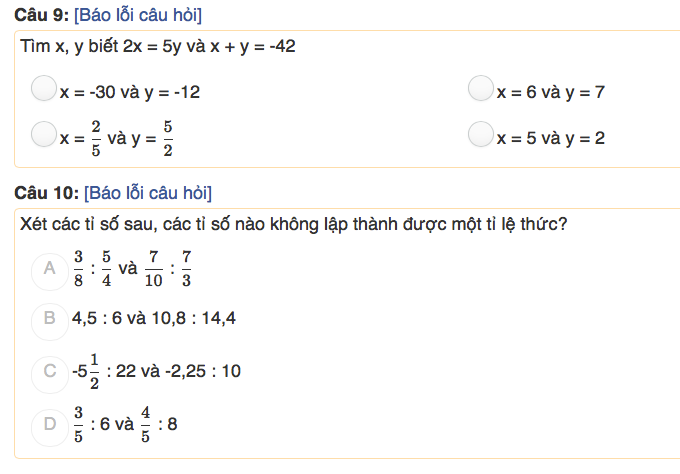
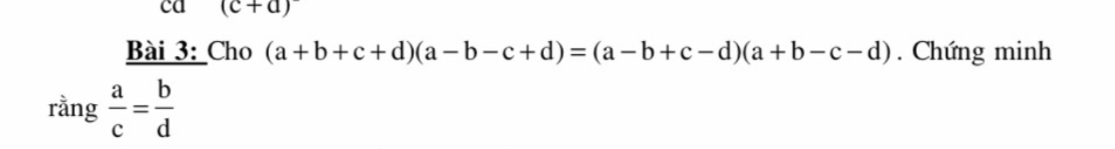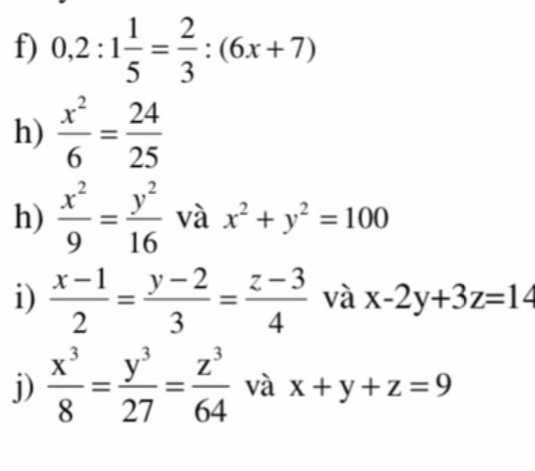\(a,\) Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2}{d^2}\\ \dfrac{a^2-b^2}{c^2-d^2}=\dfrac{b^2k^2-b^2}{d^2k^2-d^2}=\dfrac{b^2\left(k^2-1\right)}{d^2\left(k^2-1\right)}=\dfrac{b^2}{d^2}\\ \Rightarrow\dfrac{ab}{cd}=\dfrac{a^2-b^2}{c^2-d^2}\)
b, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\Rightarrow\left(\dfrac{a-b}{c-d}\right)^4=\left(\dfrac{bk-b}{dk-d}\right)^4=\left(\dfrac{b\left(k-1\right)}{d\left(k-1\right)}\right)^4=\dfrac{b^4}{d^4}\\ \dfrac{a^4+b^4}{c^4+d^4}=\dfrac{b^4k^4+b^4}{d^4k^4+d^4}=\dfrac{b^4\left(k^4+1\right)}{d^4\left(k^4+1\right)}=\dfrac{b^4}{d^4}\\ \RightarrowĐpcm\)
c, Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\Rightarrow a=bk;c=dk\)
\(\dfrac{ab}{cd}=\dfrac{bk\cdot b}{dk\cdot d}=\dfrac{b^2}{d^2}\\ \dfrac{\left(a+b\right)^2}{\left(c+d\right)^2}=\dfrac{\left(bk+b\right)^2}{\left(dk+d\right)^2}=\dfrac{\left[b\left(k+1\right)\right]^2}{\left[d\left(k+1\right)\right]^2}=\dfrac{b^2\left(k+1\right)^2}{d^2\left(k+1\right)^2}=\dfrac{b^2}{d^2}\\ \RightarrowĐpcm\)






 Giúp mình với
Giúp mình với