\(\dfrac{3x-1}{5-x}=\dfrac{3-6x}{2x+3}\) (Đk: x ≠ 5; x ≠ \(\dfrac{-3}{2}\))
=> (3x-1)(2x+3) = (3-6x)(5-x)
=> 6x2 + 7x - 3 = 15 - 33x + 6x2
=> 40x = 18
=> x = \(\dfrac{9}{20}\)(thỏa mãn điều kiện)
Vậy, x = \(\dfrac{9}{20}\)
Giúp mình câu này nhé! Thanks
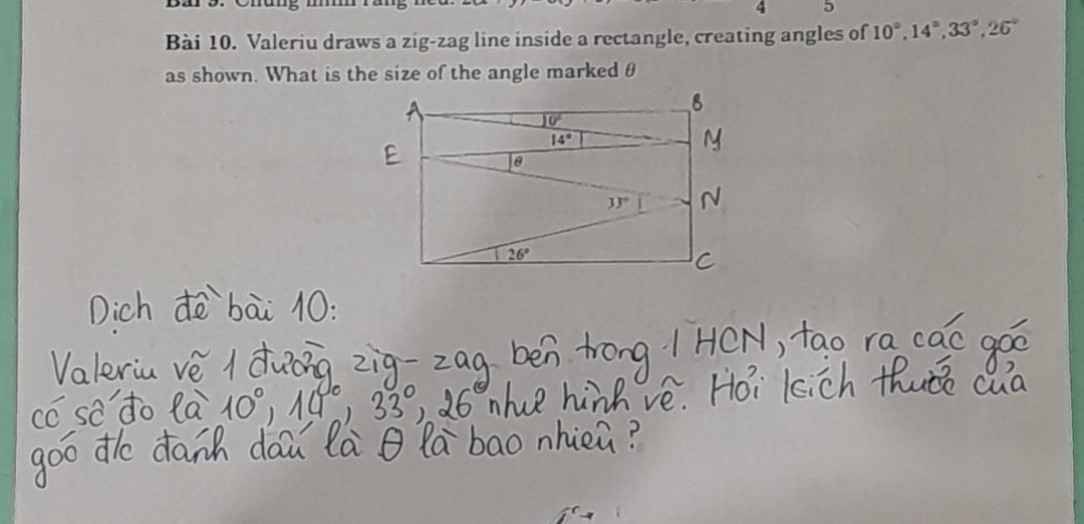Nhờ các bạn giải giúp mình 2 bài này nha cảm ơn csc bạn nhiều!!!!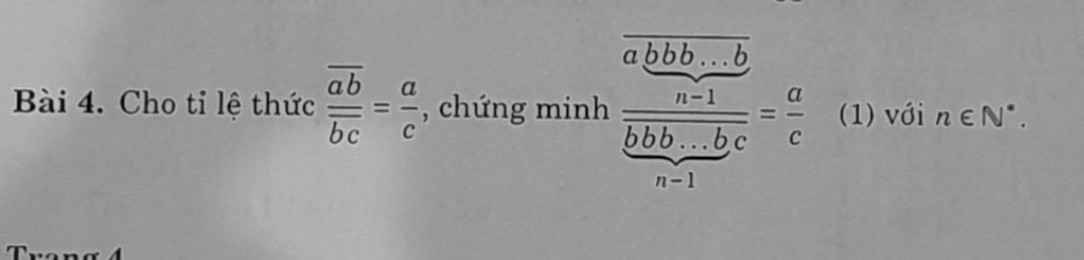
Mọi người giúp mình nốt các câu sau với ạ
Cảm ơn mọi người nhiều!
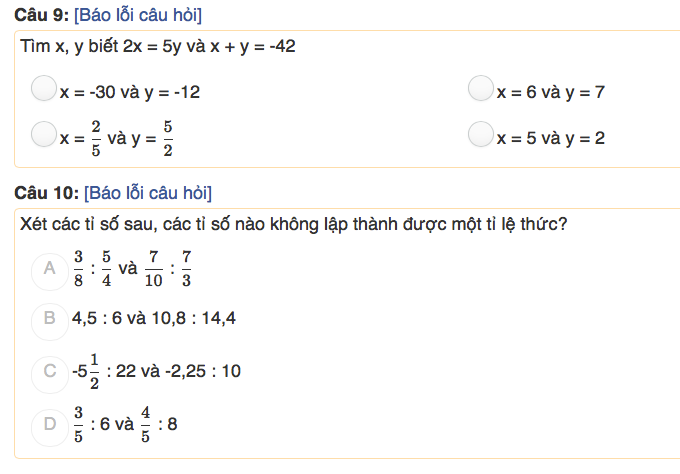
Mọi người ơi~ Giúp mình câu này với!
1. Các đẳng thức sau đây có phải tỉ lệ thức hay ko?
a)1,5 : 6 và 0,5 :2 b) -7/5 và -4/3
Cảm ơn mọi người nhiều!
cho \(\dfrac{a}{b}=\dfrac{b}{c}=\dfrac{c}{d}\)
chứng minh \(\left(\dfrac{a+b+c}{b+c+d}\right)_3=\dfrac{a}{d}\)
giúp mình với
Chứng minh rằng:
\(\dfrac{a-c}{b-d}\)=\(\dfrac{a+c}{b+d}\)
Vì chưa học công thức tính chất dãy tỉ số bằng nhau nên giúp mk giải chi tiết nha!c ơn ạ!
Chứng minh rằng từ tỉ lệ thức \(\dfrac{a}{b}=\dfrac{c}{d}\) (a - b ≠ 0, c - d ≠ 0) ta có thể suy ra được \(\dfrac{a+b}{a-b}=\dfrac{c+d}{c-d}\)
Giúp e câu cuối cùng với ah, 23h58 là e phải nộp ròi ah
câu 1 tìm A biết
\(A=\dfrac{a}{b+c}=\dfrac{c}{a+b}=\dfrac{b}{a+c}\)
câu 2
x∈Z để A∈Z
\(A=\dfrac{x+3}{x-2}\)
\(A=\dfrac{1-2x}{x+3}\)
nếu ai giải được mình cho 1 like
(x+1/2)^2=1
tìm x ạ giúp minh với mình cần gấp ạ
