1.2. pp thế
`a)`\(\left\{{}\begin{matrix}x-2\sqrt{2}y=\sqrt{5}\\x\sqrt{2}+y=\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\)\(\left\{{}\begin{matrix}x-2\sqrt{2}y=\sqrt{5}\\y=\sqrt{2}-x\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-2\sqrt{2}\left(\sqrt{2}-x\sqrt{2}\right)=\sqrt{5}\\y=\sqrt{2}-x\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x-4+4x=\sqrt{5}\\y=\sqrt{2}-x\sqrt{2}\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=\dfrac{\sqrt{5}+4}{5}\\y=-\dfrac{\sqrt{10}+\sqrt{2}}{5}\end{matrix}\right.\)
`b)`\(\left\{{}\begin{matrix}\left(\sqrt{2}-1\right)x-y=\sqrt{2}\\x+\left(\sqrt{2}+1\right)y=1\end{matrix}\right.\)
`<=>`\(\left\{{}\begin{matrix}\left(\sqrt{2}-1\right)\left(1-\left(\sqrt{2}+1\right)y\right)-y=\sqrt{2}\\x=1-\left(\sqrt{2}+1\right)y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}\sqrt{2}-1-y-y=\sqrt{2}\\x=1-\left(\sqrt{2}+1\right)y\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}y=-\dfrac{1}{2}\\x=\dfrac{3+\sqrt{2}}{2}\end{matrix}\right.\)








 ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn
ai giúp mình giải với mình cần câu c với câu d thôi cũng đc ạ! cảm ơn 




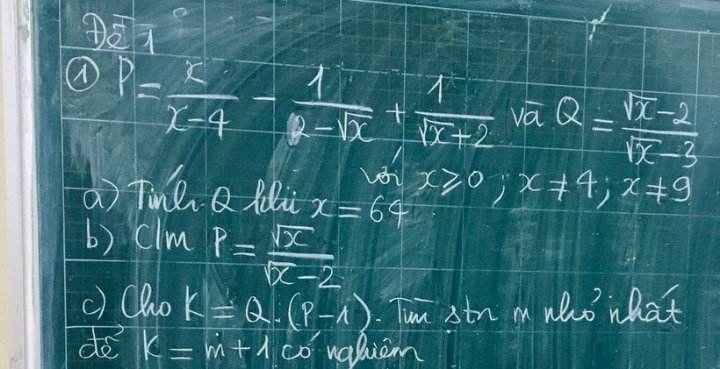 giúp mình câu c với ạ, mình cảm ơn nhiều
giúp mình câu c với ạ, mình cảm ơn nhiều