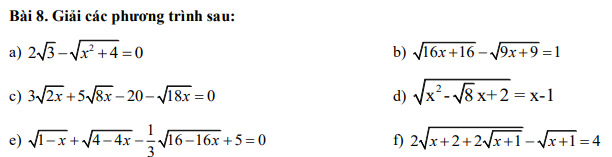a.
$2\sqrt{3}-\sqrt{x^2+4}=0$
$\Leftrightarrow 2\sqrt{3}=\sqrt{x^2+4}$
$\Leftrightarrow 12=x^2+4$
$\Leftrightarrow 8=x^2$
$\Leftrightarrow x=\pm 2\sqrt{2}$
b. ĐKXĐ: $x\geq -1$
$\sqrt{16(x+1)}-\sqrt{9(x+1)}=1$
$\Leftrightarrow 4\sqrt{x+1}-3\sqrt{x+1}=1$
$\Leftrightarrow \sqrt{x+1}=1$
$\Leftrightarrow x+1=1$
$\Leftrightarrow x=0$ (tm)
c. ĐKXĐ: $x\geq 0$
$3\sqrt{2x}+5\sqrt{8x}-20-\sqrt{18x}=0$
$\Leftrightarrow 3\sqrt{2x}+10\sqrt{2x}-20-3\sqrt{2x}=0$
$\Leftrightarrow 10\sqrt{2x}-20=0$
$\Leftrightarrow \sqrt{2x}=2$
$\Leftrightarrow 2x=4$
$\Leftrightarrow x=2$ (tm)
d.
PT \(\Rightarrow \left\{\begin{matrix} x-1\geq 0\\ x^2-\sqrt{8x}+2=(x-1)^2\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} x\geq 1\\ x=\frac{1+\sqrt{2}}{2}\end{matrix}\right.\Leftrightarrow x=\frac{1+\sqrt{2}}{2}\)
e. ĐKXĐ: $x\leq 1$
PT $\Leftrightarrow \sqrt{1-x}+2\sqrt{1-x}-\frac{4}{3}\sqrt{1-x}+5=0$
$\Leftrightarrow \frac{5}{3}\sqrt{1-x}=-5< 0$ (vô lý)
Vậy pt vô nghiệm.
f. ĐKXĐ: $x\geq -1$
PT $\Leftrightarrow 2\sqrt{(\sqrt{x+1}+1)^2}-\sqrt{x+1}=4$
$\Leftrightarrow 2(\sqrt{x+1}+1)-\sqrt{x+1}=4$
$\Leftrightarrow \sqrt{x+1}=2$
$\Leftrightarrow x=3$ (tm)
a) Ta có: \(2\sqrt{3}-\sqrt{x^2+4}=0\)
\(\Leftrightarrow\sqrt{x^2+4}=2\sqrt{3}\)
\(\Leftrightarrow x^2+4=12\)
\(\Leftrightarrow x^2=8\)
hay \(x\in\left\{2\sqrt{2};-2\sqrt{2}\right\}\)
b) Ta có: \(\sqrt{16x+16}-\sqrt{9x+9}=1\)
\(\Leftrightarrow4\sqrt{x+1}-3\sqrt{x+1}=1\)
\(\Leftrightarrow\sqrt{x+1}=1\)
\(\Leftrightarrow x+1=1\)
hay x=0
c) Ta có: \(3\sqrt{2x}+5\sqrt{8x}-20-\sqrt{18x}=0\)
\(\Leftrightarrow3\sqrt{2x}+10\sqrt{2x}-3\sqrt{2x}=20\)
\(\Leftrightarrow2x=4\)
hay x=2
d) Ta có: \(\sqrt{x^2-2\sqrt{2x}+2}=x-1\)
\(\Leftrightarrow x^2-2\sqrt{2x}+2=x^2-2x+1\)
\(\Leftrightarrow2x-2\sqrt{2x}+1=0\)
\(\Leftrightarrow x=\dfrac{\sqrt{2}+1}{2}\)
e) Ta có: \(\sqrt{1-x}+\sqrt{4-4x}-\dfrac{1}{3}\sqrt{16-16x}+5=0\)
\(\Leftrightarrow\sqrt{1-x}+2\sqrt{1-x}-\dfrac{4}{3}\sqrt{1-x}=-5\)
\(\Leftrightarrow\dfrac{5}{3}\sqrt{1-x}=-5\)(Vô lý)
f) Ta có: \(2\sqrt{x+2+2\sqrt{x+1}}-\sqrt{x+1}=4\)
\(\Leftrightarrow2\sqrt{x+1+2\cdot\sqrt{x+1}\cdot1+1}-\sqrt{x+1}=4\)
\(\Leftrightarrow2\left(\sqrt{x+1}+1\right)-\sqrt{x+1}=4\)
\(\Leftrightarrow\sqrt{x+1}+2=4\)
\(\Leftrightarrow x+1=4\)
hay x=3