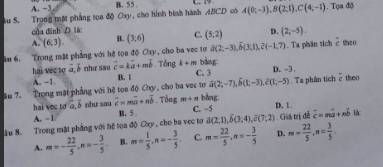Câu 4:
ĐKXĐ: m<>-3
Để phương trình có hai nghiệm phân biệt thì \(\left(2m+12\right)^2-4\left(m+3\right)\left(m+14\right)>0\)
\(\Leftrightarrow4m^2+48m+144-4m^2-68m-168>0\)
=> -20m-24>0
hay m<-6/5
Theo đề, ta có:
\(\left\{{}\begin{matrix}3x_1-x_2=0\\x_1+x_2=\dfrac{2\left(m+6\right)}{m+3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}4x_1=\dfrac{2\left(m+6\right)}{m+3}\\x_2=3x_1\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x_1=\dfrac{m+6}{2m+6}\\x_2=\dfrac{3m+18}{2m+6}\end{matrix}\right.\)
Ta có: \(x_1\cdot x_2=\dfrac{m+14}{m+3}\)
\(\Leftrightarrow3\left(m+6\right)^2\left(m+3\right)=\left(2m+6\right)^2\left(m+14\right)\)
Đến đây bạn chỉ cần giải phương trình tìm m là xong rồi
5.
Do tam giác ABC cân tại A \(\Rightarrow\) H đồng thời là trung điểm BC
\(\Rightarrow BH=CH=\dfrac{1}{2}BC=2a\)
Trong tam giác vuông ACH:
\(AH=CH.tanC=2a.tan30^0=\dfrac{2a\sqrt{3}}{3}\)
\(\Rightarrow\overrightarrow{AH}.\overrightarrow{BA}=\overrightarrow{AH}.\left(\overrightarrow{BH}+\overrightarrow{HA}\right)=\overrightarrow{AH}.\overrightarrow{BH}-\overrightarrow{AH}.\overrightarrow{AH}\)
\(=0-AH^2=-AH^2=-\dfrac{4a^2}{3}\)
7.
Ta có:
\(\dfrac{a}{b+c}+\dfrac{b}{c+a}+\dfrac{c}{a+b}=\dfrac{a^2}{ab+ac}+\dfrac{b^2}{bc+ab}+\dfrac{c^2}{ac+bc}\)
\(\ge\dfrac{\left(a+b+c\right)^2}{2\left(ab+bc+ca\right)}\ge\dfrac{3\left(ab+bc+ca\right)}{2\left(ab+bc+ca\right)}=\dfrac{3}{2}\) (đpcm)
Dấu "=" xảy ra khi \(a=b=c\)