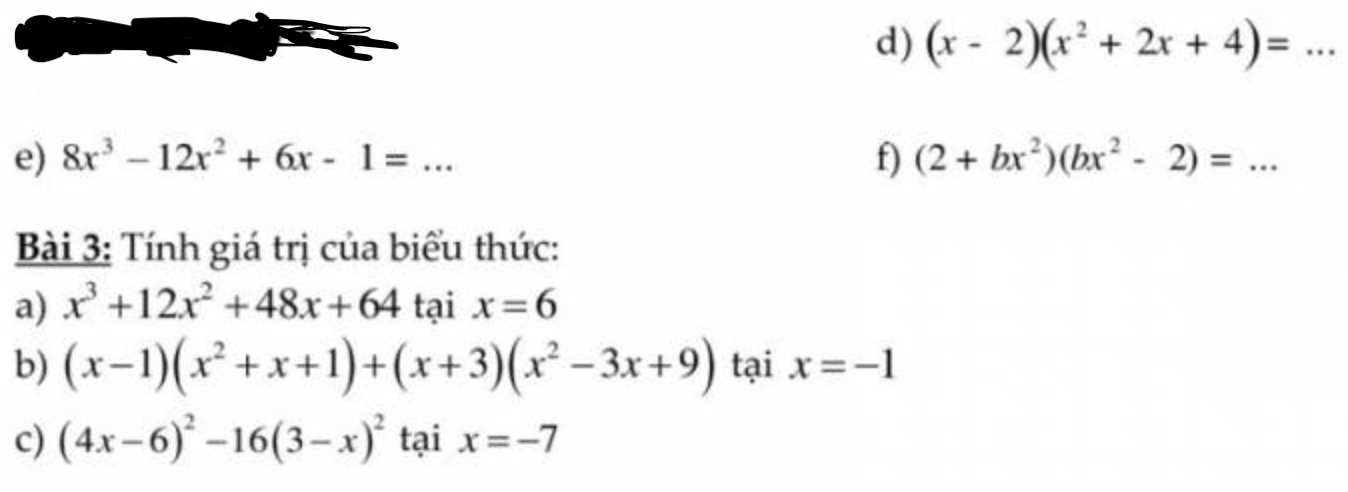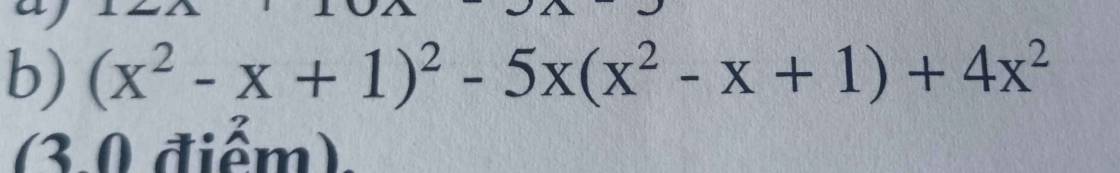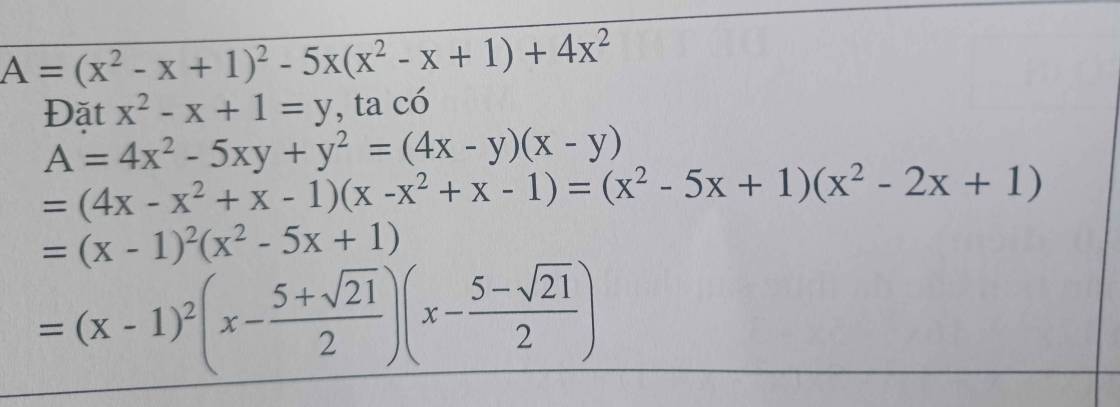\(a,4x^2-6x=2x\left(2x-3\right).\\ b,3x\left(x-1\right)+5\left(x-1\right).\\ =\left(3x+5\right)\left(x-1\right).\\ c,\dfrac{1}{3}x^4y^3+3x^2y^4-x^2y^3.\\ =x^2y^3\left(\dfrac{1}{3}x^2+3y-1\right).\)
\(d,x\left(x+y\right)-5x-5y.\\ =x\left(x+y\right)-5\left(x+y\right).\\ =\left(x-5\right)\left(x+y\right).\\ e,-6x\left(x-1\right)+30\left(x-1\right)^2.\\ =6\left(x-1\right)\left(-x+5x-5\right).\\ =6\left(x-1\right)\left(4x-5\right).\)
\(f,\dfrac{1}{2}xy\left(x-y\right)^2-xy^2\left(y-x\right)+\left(y-x\right).\\ =\dfrac{1}{2}xy\left(x-y\right)^2+xy^2\left(x-y\right)-\left(x-y\right).\\ =\left(x-y\right)\left[\dfrac{1}{2}xy\left(x-y\right)+xy^2-1\right].\\ =\left(x-y\right)\left(\dfrac{1}{2}x^2y-\dfrac{1}{2}xy^2+xy^2-1\right).\\ =\left(x-y\right)\left(\dfrac{1}{2}x^2y+\dfrac{1}{2}xy^2-1\right).\)













 Giúp em câu này vs ạ
Giúp em câu này vs ạ
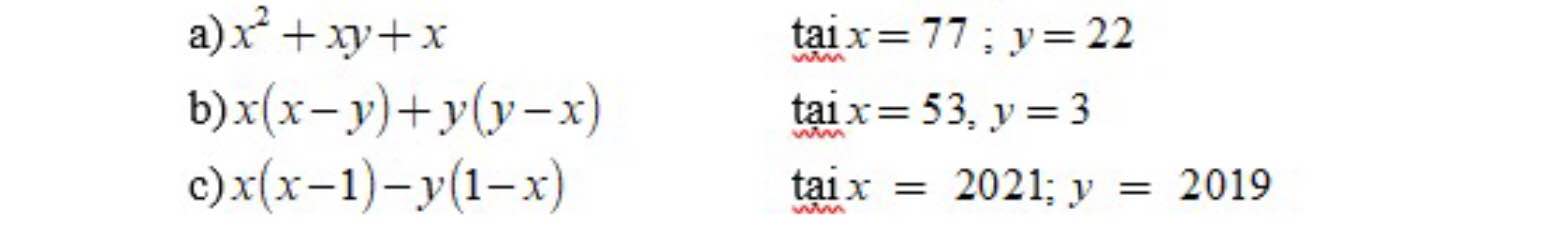 bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ
bài này nữa thôi các anh chị :3 em cảm ơn nhiều ạ