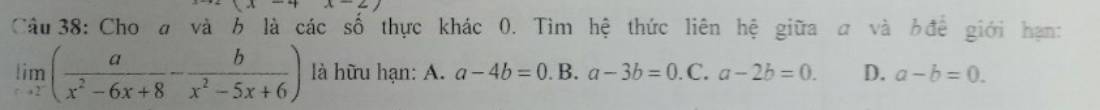Question

Giới hạn \(x\rightarrow2^-\)

Answer 1

\(\dfrac{a}{\left(x-2\right)\left(x-4\right)}-\dfrac{b}{\left(x-2\right)\left(x-3\right)}=\dfrac{a\left(x-3\right)-b\left(x-4\right)}{\left(x-2\right)\left(x-3\right)\left(x-4\right)}\)

\(=\dfrac{ax-3a-bx+4b}{\left(x-2\right)\left(x-3\right)\left(x-4\right)}=\dfrac{\left(a-b\right)x-\left(3a-4b\right)}{\left(x-2\right)\left(x-3\right)\left(x-4\right)}\)

Giới hạn hữu hạn khi \(\left(a-b\right)x-\left(3a-4b\right)=0\) có nghiệm \(x=2\)

\(\Rightarrow2\left(a-b\right)-\left(3a-4b\right)=0\Rightarrow a-2b=0\)