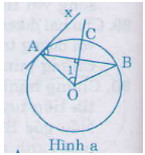
Theo giả thiết,
Suy ra: 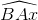 =
= 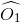
Hai góc nhọn này đã có một cặp cạnh vuông góc với nhau ( OC ⊥ AB).
Vậy cặp cạnh kia cũng phải vuông góc, tức là OA ⊥ Ax.
Vậy Ax phải là tiếp tuyến của (O) tại A

Theo giả thiết,
Suy ra: 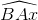 =
= 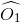
Hai góc nhọn này đã có một cặp cạnh vuông góc với nhau ( OC ⊥ AB).
Vậy cặp cạnh kia cũng phải vuông góc, tức là OA ⊥ Ax.
Vậy Ax phải là tiếp tuyến của (O) tại A
Từ điểm A ở ngoài đường tròn (O) vẽ 2 tiếp tuyến AB, AC và cát tuyến AMN của đường tròn đó. Gọi I là trung điểm của dây MN.
a) Chứng minh: Năm điểm A, B, I, O, C cùng nằm trên một đường tròn, xác định tâm và bán kính của đường tròn này.
b) Vẽ đường kính BD. Chứng minh CD song song với OA.
Cho đường tròn (O; R) và dây cung BC = R. Hai tiếp tuyến của đường tròn (O) tại B, C cắt nhau tại A. Tính góc ABC và góc BAC
Cho đường tròn (O;R) và dây cung BC=R . Hai tiếp tuyến của đường tròn (O) tại B,C cắt nhau ở A . Tính góc ABC và góc BAC
Hai tiếp tuyến tại a và b của đường tròn cắt nhau tại S biết góc asb = 50° thì số đo của cung nhỏ AB bằng:a.130° b.310° c.50° d.230°
Cho điểm P nằm ngoài [O] ,vẽ tiếp tuyến PA và cát tuyến PBC của đường tròn .Tia phân giác của góc BAC cắt dây BC tại D .Chứng minh PA=PD
Cho nửa đường tròn tâm O đường kính AB = 2R ( R là một độ dài cho trước). Gọi C, D là hai điểm trên nửa đường tròn đó sao cho C thuộc cung AD và góc COD = 120. gọi giao điểm của hai dây AD và BC là E, giao điểm của các đường thẳng AC và BD là Fa) Chứng minh 4 điểm C, D, E, F cùng nằm trên một đường tròn
b) Tính góc IOD
c) CM ID là tiếp tuyến của đường tròn tâm O
Cho nửa đường tròn tâm O đường kính AB = 2R ( R là một độ dài cho trước). Gọi C, D là hai điểm trên nửa đường tròn đó sao cho C thuộc cung AD và góc COD = 120. gọi giao điểm của hai dây AD và BC là E, giao điểm của các đường thẳng AC và BD là Fa) Chứng minh 4 điểm C, D, E, F cùng nằm trên một đường tròn
b) Tính góc IOD
c) Chứng minh ID là tiếp tuyến của đường tròn tâm O