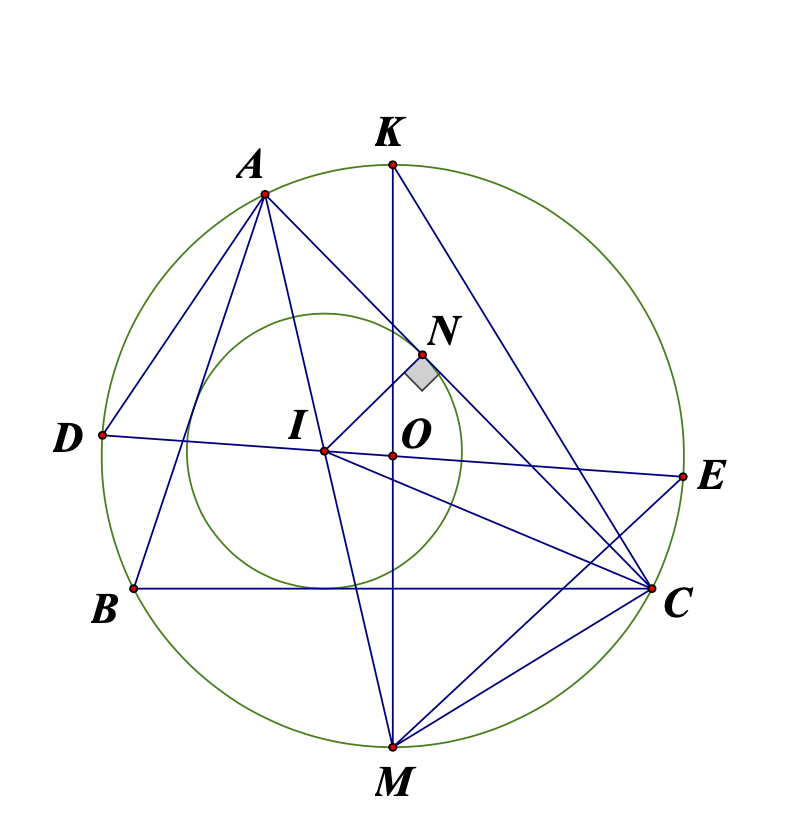
a: Xét ΔAMB vuông tại M và ΔAKS vuông tại K có
góc MAB chung
=>ΔAMB đồng dạng với ΔAKS
=>AM*AS=AK*AB
Xét ΔBNA vuông tại N và ΔBKS vuông tại K có
góc NBA chung
=>ΔBNA đồng dạng với ΔBKS
=>BN*BS=BK*BA
=>AM*AS+BN*BS=4*R^2
b: \(S_{q\left(MN\right)}=pi\cdot R^2\cdot\dfrac{60}{360}=\dfrac{1}{6}\cdot pi\cdot R^2\)
\(S_{OMN}=R^2\cdot\dfrac{\sqrt{3}}{2}\)
=>\(S_{vp\left(MN\right)}=R^2\left(\dfrac{1}{6}pi-\dfrac{\sqrt{3}}{2}\right)\)
Xét ΔSAB có MN//AB
nên SM/SA=SN/SB=MN/AB=1/2
=>SM=1/2SA; SN=1/2SB
=>M là trung điểm của SA, N là trung điểm của SB
=>ΔSAB đều
=>\(S_{SAB}=\left(2R\right)^2\cdot\dfrac{\sqrt{3}}{4}=R^2\sqrt{3}\)
SM=SN=MN=R
=>ΔSMN đều
=>\(S_{SMN}=\dfrac{R^2\sqrt{3}}{4}\)
=>\(S_{CMNB}=\dfrac{3R^2\sqrt{3}}{4}\)
DIện tích tam giác SAB phần nằm ngoài (O) là:
\(R^2\sqrt{3}-R^2\left(\dfrac{1}{6}pi-\dfrac{\sqrt{3}}{2}\right)-R^2\cdot\dfrac{3\sqrt{3}}{4}\)