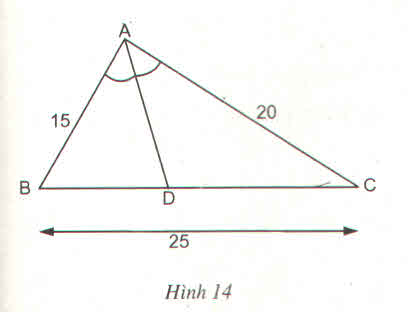
a) Theo t/c đường phân giác, có:
\(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)
hay \(\dfrac{DB}{21}=\dfrac{DC}{28}=\dfrac{DB+DC}{49}=\dfrac{BC}{49}\)\(=\dfrac{\sqrt{21^2+28^2}}{49}=\dfrac{35}{49}=\dfrac{5}{7}\)
\(\Rightarrow DB=\dfrac{5}{7}.21=15\left(cm\right)\)\(;DC=\dfrac{5}{7}.28=20\left(cm\right)\)
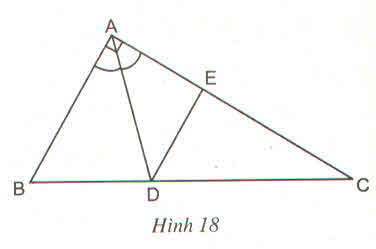
Có: DE//AB
\(\Rightarrow\Delta_vCDE\sim\Delta_vCBA\left(gn\right)\)
\(\Rightarrow\dfrac{DE}{AB}=\dfrac{DC}{BC}=\dfrac{20}{35}=\dfrac{4}{7}\)
\(\Rightarrow DE=\dfrac{4}{7}.21=12\left(cm\right)\)
b) Kẻ AK \(\perp BC\)
Có: \(\dfrac{S_{ABD}}{S_{ACD}}=\dfrac{\dfrac{1}{2}AK.BD}{\dfrac{1}{2}AK.CD}\)\(\dfrac{DB}{CD}=\dfrac{15}{20}=\dfrac{3}{4}\)