Question

Cho ΔABC ⊥ A, AB = 21cm, đường phân giác của góc A cắt BC tại D, đường thẳng qua D và song song với AB cắt AC tại E

a) Tính độ dài BD, DC, DE.

b) Tính diện tích tam giác ABD và tam giác ACD.

Answer 1

Bổ sung đề: AC=28cm

a) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:

\(BC^2=AB^2+AC^2\)

\(\Leftrightarrow BC^2=21^2+28^2=1225\)

hay BC=35(cm)

Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)

nên \(\dfrac{DB}{AB}=\dfrac{DC}{AC}\)(Tính chất đường phân giác của tam giác)

\(\Leftrightarrow\dfrac{DB}{21}=\dfrac{DC}{28}\)

mà DB+DC=BC(D nằm giữa B và C)

nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:

\(\dfrac{DB}{21}=\dfrac{DC}{28}=\dfrac{DB+DC}{21+28}=\dfrac{35}{49}=\dfrac{5}{7}\)

Do đó:

\(\left\{{}\begin{matrix}\dfrac{BD}{21}=\dfrac{5}{7}\\\dfrac{CD}{28}=\dfrac{5}{7}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=15\left(cm\right)\\CD=20\left(cm\right)\end{matrix}\right.\)

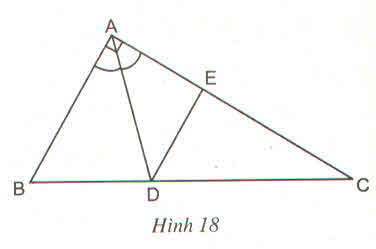
Xét ΔABC có 

D∈BC(gt)

E∈AC(gt)

DE//AB(gt)

Do đó: \(\dfrac{DE}{AB}=\dfrac{CD}{CB}\)(Hệ quả Định lí Ta lét)

\(\Leftrightarrow\dfrac{DE}{21}=\dfrac{20}{35}\)

hay \(DE=\dfrac{21\cdot20}{35}=\dfrac{420}{35}=12\left(cm\right)\)

Vậy: CD=15cm; BD=20cm; DE=12cm