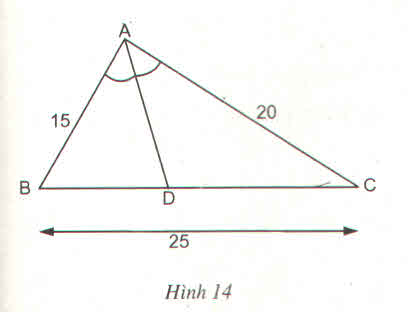
Trong ΔABC, ta có: AD là đường phân giác của (BAC)
Suy ra: \(\frac{DB}{DC}=\frac{AB}{AC}\)(tính chất đường phân giác)
Mà AB = 15 (cm); AC = 20 (cm)
Nên \(\frac{DB}{DC}=\frac{15}{20}\)
uy ra: \(\frac{DB}{DB+DC}=\frac{15}{15+20}\)(tính chất tỉ lệ thức)
Suy ra: \(\frac{DB}{BC}=\frac{15}{35}\Rightarrow DB=\frac{15}{35}.BC=\frac{15}{35}.25=\frac{75}{7}cm\)
\(\Rightarrow DC=BC-BD=25-\frac{75}{7}=\frac{100}{7}cm\)
b. Kẻ AH ⊥ BC
Ta có: SABD = 1/2 AH.BD; SADC = 1/2 AH.DC
Suy ra :\(\frac{S_{ABD}}{S_{ADC}}=\frac{\frac{1}{2}AH.BD}{\frac{1}{2}AH.DC}=\frac{BD}{DC}\)
Mà\(\frac{DB}{DC}=\frac{15}{20}=\frac{3}{4}\)
\(\Rightarrow\frac{S_{ABD}}{S_{ADC}}=\frac{3}{4}\)