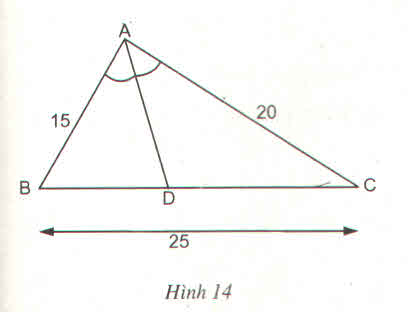
a) △ABC có AD là đường phân giác
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{DB}{DC}\) (t/c)
\(\Rightarrow\dfrac{DB}{DC}=\dfrac{6}{9}=\dfrac{2}{3}\Rightarrow3DB=2DC\)
Mà \(BD+CD=BC=10\)
\(\Rightarrow2BD+2CD=5BD=20\\ \Rightarrow BD=4\left(cm\right)\)
△ABC có AE là đường phân giác ngoài tại đỉnh A
\(\Rightarrow\dfrac{AB}{AC}=\dfrac{EB}{EC}\) (T/c)
\(\Rightarrow\dfrac{EB}{EC}=\dfrac{6}{9}=\dfrac{2}{3}\Rightarrow3EB=2EC\)
Mà \(EC=EB+BC=EB+10\)
\(\Rightarrow2EB+20=2EC=3EB\\ \Rightarrow BE=20\left(cm\right)\)
b) △ABC có AD là đường phân giác trong
AE là đường phân giác ngoài tại đỉnh A
\(\Rightarrow AD\perp AE\) → △ADE vuông tại A
c) Kẻ AH ⊥ BC
\(S_{ADB}=\dfrac{AH}{2}\cdot BD\)
\(S_{ADC}=\dfrac{AH}{2}\cdot CD\)
Mà \(DB=\dfrac{2}{3}DC\)
\(\Rightarrow S_{ADB}=\dfrac{2}{3}S_{ADC}\)
b) Vì AD là phân giác góc BAC (gt) => ^BAD = ^DAC
Gọi tia đối của AC là d
Vì AE là phân giác ^dAB (gt) => ^dAE = ^EAB
Tá có: ^BAD + ^DAC + ^dAE + ^EAB = 180o
=> 2 ^EAB + 2 ^BAD = 180o
<=> ^EAB + ^BAD = 90o
<=> ^EAD = 90o
Xét tam giác ADE: ^EAD = 90o (cmt)
=> tam giác ADE vuông tại A (đpcm)
a) Xét ΔABC có AD là đường phân giác ứng với cạnh BC(gt)
nên \(\dfrac{BD}{AB}=\dfrac{DC}{AC}\)(Tính chất đường phân giác của tam giác)
hay \(\dfrac{BD}{6}=\dfrac{DC}{9}\)
mà BD+CD=BC(D nằm giữa B và C)
nên Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{6}=\dfrac{DC}{9}=\dfrac{BD+DC}{6+9}=\dfrac{BC}{15}=\dfrac{10}{15}=\dfrac{2}{3}\)
Do đó: \(\left\{{}\begin{matrix}\dfrac{BD}{6}=\dfrac{2}{3}\\\dfrac{CD}{9}=\dfrac{2}{3}\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BD=4\left(cm\right)\\CD=6\left(cm\right)\end{matrix}\right.\)
hay BD=4(cm)
Vậy: DB=4cm
Từ A kẻ đường cao AH của tam giác ABC
Ta có: BC = BD + DC
Thay số: 10 = 4 + DC
=> DC = 6 (cm)
Ta có: S ABD = 1/2 AH . BD
S ADC = 1/2 AH . DC
=> \(\dfrac{\text{S ABD}}{\text{S ADC}}=\dfrac{\dfrac{1}{2}AH.BD}{\dfrac{1}{2}AH.DC}=\dfrac{BD}{DC}=\dfrac{4}{6}=\dfrac{2}{3}\)