a: Xét ΔABC có AD là đường phân giác
nên BD/AB=CD/AC
hay BD/15=CD/20
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{15}=\dfrac{CD}{20}=\dfrac{BD+CD}{15+20}=\dfrac{25}{35}=\dfrac{5}{7}\)
Do đó: BD=75/7; CD=100/7
a: Xét ΔABC có AD là đường phân giác
nên BD/AB=CD/AC
hay BD/15=CD/20
Áp dụng tính chất của dãy tỉ số bằng nhau, ta được:
\(\dfrac{BD}{15}=\dfrac{CD}{20}=\dfrac{BD+CD}{15+20}=\dfrac{25}{35}=\dfrac{5}{7}\)
Do đó: BD=75/7; CD=100/7
Tam giác ABC có AB = 15cm, AC = 20 cm, BC = 25 cm. Đường phân giác góc BAC cắt cạnh ABC tại D (h.14)
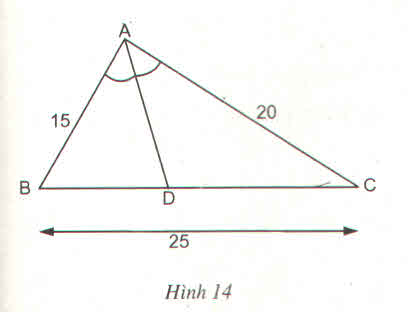
a) Tính độ dài các đoạn thẳng DB và DC
b) Tính tỉ số diện tích của hai tam giác ABD và ACD
cho tam giác ABC cân tại A biết AB=15cm.BC=10cm,phân giác góc B cắt AC tại D.
a) tính AD,CD
b)tính tỉ số diện tích tam giác ABD và tam giác BCD.
Bài 3 (3 điểm): Cho ∆ABC có:
![]()
Kẻ đường cao AH (H ∈ BC ), tia phân giác góc A cắt BC tại D.
a) Chứng minh ∆HBA đồng dạng với ∆ABC và AB2 = BH.BC
b) Tính độ dài BC, BD và CD.
c) Tính tỉ số diện tích tam giác ABD và tam giác ACD.
d) Từ D kẻ DE vuông góc với AC (E ∈ AC). Tính độ dài đoạn DE.
Cho ΔABC ⊥ A, AB = 21cm, đường phân giác của góc A cắt BC tại D, đường thẳng qua D và song song với AB cắt AC tại E
a) Tính độ dài BD, DC, DE.
b) Tính diện tích tam giác ABD và tam giác ACD.
Cho tam giác ABC có AB=6cm, AC=9cm, BC=10cm, đường phân giác trong AD, đường phân giác ngoài AE.
a. Tính DB, EB.
b. CM tam giác ADE vuông
c. Tính tỉ số diện tích của tam giác ABD và tam giác ADC
Cho tam giác vuông ABC ( \(\widehat{A}=90^0\)), AB = 21 cm, AC = 28 cm; đường phân giác góc A cắt BC tại D, đường thẳng qua D và song song với AB, cắt AC tại E (h.18)
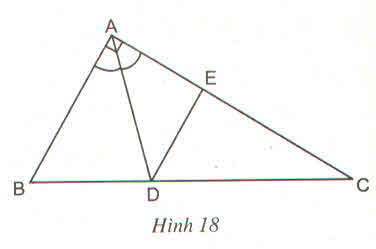
a) Tính độ dài các đoạn thẳng BD, DC và DE
b) Tính diện tích tam giác ABD và diện tích tam giác ACD
Cho Tam Giác ABC vuông tại A biết AB = 21 cm, AC = 28 cm, phân Giác AD ( D thuộc BC)
a) Tính độ Dài DB DC
b) Gọi E là hình chiếu của D trên AC. Hãy Tính Độ dài DE EC
c) C/m tam giác ABC đồng dạng với tam giác EDC. Tính tỉ số đồng dạng
Tam giác ABC có AB = 12 cm, AC = 20 cm, BC = 28 cm. Đường phân giác góc A cắt BC tại D. Qua D kẻ DE // AB (E thuộc AC) (h.17)

a) Tính độ dài các đoạn thẳng BD, DC và DE
b) Cho biết diện tích tam giác ABC là S, tính diện tích các tam giác ABD, ADE và DCE