Do BD là tia phân giác của ∠ABC (gt)
⇒ ∠ABD = ∠CBD
⇒ ∠ABD = ∠HBD
Xét hai tam giác vuông: ∆ABD và ∆HBD có:
BD là cạnh chung
∠ABD = ∠HBD (cmt)
⇒ ∆ABD = ∆HBD (cạnh huyền - góc nhọn)
⇒ AD = DH (hai cạnh tương ứng)
Xét hai tam giác vuông: ∆ADK và ∆HDC có:
AD = DH (cmt)
∠ADK = ∠HDC (đối đỉnh)
⇒ ∆ADK = ∆HDC (cạnh góc vuông - góc nhọn kề)
⇒ AK = HC (hai cạnh tương ứng)
Do ∆ABD = ∆HBD (cmt)
⇒ AB = HB (hai cạnh tương ứng)
Mà AK = HC (cmt)
⇒ AB + AK = HB + HC
⇒ BK = BC
Do I là trung điểm của KC (gt)
⇒ IK = IC
Xét ∆BCI và ∆BKI có:
BC = BK (cmt)
IC = IK (cmt)
BI là cạnh chung
⇒ ∆BCI = ∆BKI (c-c-c)
⇒ ∠IBC = ∠IKC (hai góc tương ứng)
⇒ BI là tia phân giác của ∠KBC
⇒ BI là tia phân giác của ∠ABC
Mà BD là tia phân giác của ∠ABC (gt)
⇒ B, D, I thẳng hàng
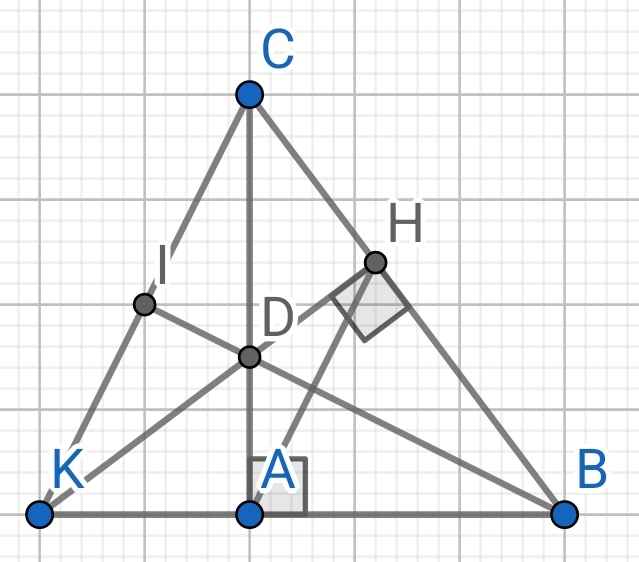
Sửa đề:cho tam giác abc vuông tại a dường phân giác bd ( d thuộc ac ) từ d kẻ dh vuông góc với bc gọi k là giao điểm của đường thẳng ab và hd,i là trung điểm của kc . chứng minh 3 điểm b,d,i thẳng hàng
Giải
Xét △BAD và △BHD có:BD chung
DAB^=DHB^=90°
ABD^=HBD^
⇒△BAD = △BHD
⇒BA=BH
Xét △BAC và △BHK có: BA=BH
BHK^=BAC^=90°
B^ chung
⇒△BAC = △BHK
⇒BK=BC
Xét △BIC và △BIK có: IK=IC
BK=BC
BI chung
⇒△BIC = △BIK
⇒BIK^=BIC^
mà 2 góc này là 2 góc kề bù
⇒BIK^=BIC^=90°
⇒BI⊥KC (1)
△BKC có:KH⊥BC
CA⊥BK
KH cắt CA tại D
⇒D là trực tâm △BKC
Vì D là trực tâm △BKC nên đường cao thứ 3 đi qua D
mà đường cao thứ 3 của △BKC là BI(Do BI⊥KC)
⇒B,D,I thẳng hàng















