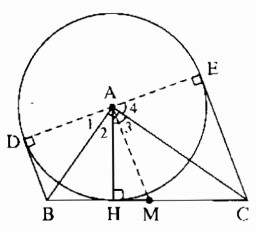
a) Theo tính chất hai tiếp tuyến cắt nhau ta có:
a) Theo tính chất hai tiếp tuyến cắt nhau ta có:
AB là tia phân giác của góc HAD
\(\Rightarrow\widehat{DAB}=\widehat{BAH}\)
AC là tia phân giác của góc HAE
\(\Rightarrow\widehat{HAD}=\widehat{CAE}\)
Ta có: \(\widehat{HAD}+\widehat{HEA}=2.\left(\widehat{BAH}+\widehat{HAC}\right)=2.\widehat{BAC}=2.90^o=180^o\)
Vậy ba điểm D, A, E thẳng hàng.
b) Gọi M là trung điểm của BC
Theo tính chất của tiếp tuyến, ta có: \(AD\downarrow BD;AE\downarrow CE\)
Suy ra: BD // CE
Vậy tứ giác BDEC là hình thang
Khi đó MA là đường trung bình của hình thang BDEC
Suy ra: \(MA\\ BD\Rightarrow MA\downarrow DE\)
Trong tam giác vuông ABC ta có: MA = MB = MC
Suy ra M là tâm đường tròn đường kính BC với MA là bán kính
Vậy DE là tiếp tuyến của đường tròn tâm M đường kính BC
a) theo tính chất 2 tiếp tuyến cắt nhau
ta có : DAB = BAH và HAC = CAE
DAH + HAE = 2(BAH + HAC) = 2.90 = 180
vậy D , A , E thẳng hàng
b) gọi M là trung diểm của BC
mà DA = AE = R
\(\Rightarrow\) MA là đường trung bình của hình thang BDEC nên MA // DB \(\Rightarrow\) MA \(\perp\) DE
mà MA = MB = MC nên MA là bán kính của đường tròn có đường kính BC
vậy DE là tiếp tuyến của đường tròn có đường kính BC
\(\Leftrightarrow\) DE tiếp xúc với đường tròn có đường kính BC (đpcm)












