Bài 6: Tính chất hai tiếp tuyến cắt nhau
Nội dung lý thuyết
1. Định lí về hai tiếp tuyến cắt nhau
Cho đường tròn \(\left(O\right)\) và một điểm \(A\) nằm ngoài đường tròn. \(AB,AC\) là các tiếp tuyến kẻ từ \(A\) đến \(\left(O\right)\) (\(B,C\) là các tiếp điểm).
Khi đó, ta gọi góc \(BAC\) là góc tạo bởi 2 tiếp tuyến \(AB,AC\); góc tạo bởi 2 bán kính \(OB,OC\) là góc \(BOC\).
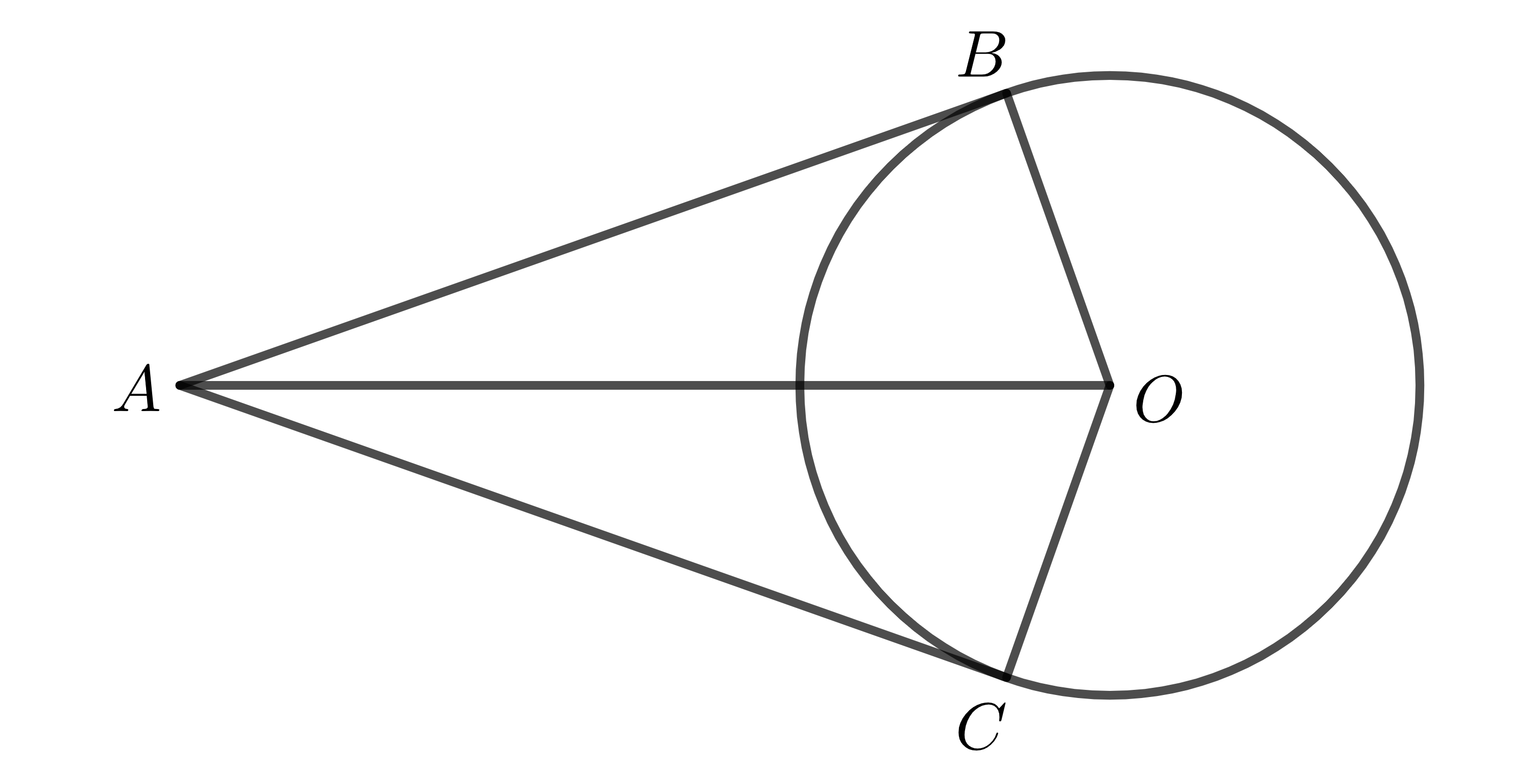
Do \(AB,AC\) là các tiếp tuyến của đường tròn \(\left(O\right)\) \(\Rightarrow AB\perp OB;AC\perp OC\).
Xét tam giác \(ABO\) và tam giác \(ACO\) có:
\(\widehat{ABO}=\widehat{ACO}=90^0\);
\(AO\) chung;
\(OB=OC\)
\(\Rightarrow\Delta ABO=\Delta ACO\) (cạnh huyền - cạnh góc vuông)
\(\Rightarrow\left\{{}\begin{matrix}AB=AC\\\widehat{BAO}=\widehat{CAO}\\\widehat{BOA}=\widehat{COA}\end{matrix}\right.\) (các cạnh và góc tương ứng).
Các kết quả trên không phụ thuộc vào cách chọn đường tròn và vị trí của điểm \(A\).
Như vậy, ta có kết quả được phát biểu trong định lí sau:
Định lí: Nếu hai tiếp tuyến của một đường tròn cắt nhau tại một điểm thì
- Điểm đó cách đều hai tiếp điểm.
- Tia kẻ từ điểm đó đi qua tâm là tia phân giác của góc tạo bởi hai tiếp tuyến.
- Tia kẻ từ tâm đi qua điểm đó là tia phân giác của góc tạo bởi hai bán kính đi qua các tiếp điểm.
Ví dụ: Cho đường tròn \(\left(O\right)\), điểm \(A\) nằm ngoài đường tròn. Kẻ các tiếp tuyến \(AB,AC\) với đường tròn (\(B,C\) là các tiếp điểm).
a) Chứng minh \(OA\perp BC\).
b) Tính các cạnh của tam giác \(ABC\) biết \(OA=4;OB=2\).
Lời giải:

a) Do \(AB,AC\) là hai tiếp tuyến của đường tròn \(\left(O\right)\)
\(\Rightarrow AB=AC\) (tính chất hai tiếp tuyến cắt nhau)
Mà \(OB=OC\)
\(\Rightarrow OA\) là đường trung trực của đoạn thẳng \(BC\)
\(\Rightarrow OA\perp BC\).
b) Gọi \(BC\cap OA=H\) \(\Rightarrow BC\perp OA\) tại \(H\).
Do \(AB\) là tiếp tuyến của đường tròn \(\left(O\right)\) nên \(AB\perp OB\).
Áp dụng định lí Pytago ta có:
\(AO^2=OB^2+AB^2\Rightarrow AB=AC=\sqrt{OA^2-OB^2}=\sqrt{4^2-2^2}=2\sqrt{3}\).
Mặt khác, theo câu a, ta có: \(\Delta ABC\) cân tại \(A\), \(AO\perp BC\) tại \(H\)
\(\Rightarrow AH\) là trung tuyến \(\Delta ABC\) \(\Rightarrow H\) là trung điểm \(BC\).
Áp dụng hệ thức giữa cạnh và đường cao trong tam giác vuông, ta có:
\(\dfrac{1}{BH^2}=\dfrac{1}{AB^2}+\dfrac{1}{OB^2}\Rightarrow\dfrac{1}{BH^2}=\dfrac{1}{3}\Rightarrow BH=\sqrt{3}\)
\(\Rightarrow BC=2.BH=2\sqrt{3}\).
Vậy \(AB=AC=BC=2\sqrt{3}\).
@57334@@57389@
2. Đường tròn nội tiếp tam giác
- Đường tròn nội tiếp tam giác là đường tròn tiếp xúc với cả ba cạnh của tam giác. Khi đó, tam giác được gọi là tam giác ngoại tiếp đường tròn.
- Tâm đường tròn nội tiếp tam giác là giao điểm ba đường phân giác trong của tam giác.
Cụ thể: Cho tam giác \(ABC\). Gọi \(I\) là giao điểm 3 đường phân giác trong của tam giác. \(D,E,F\) lần lượt là chân đường vuông góc kẻ từ \(I\) đến các cạnh \(BC,AC,AB\).
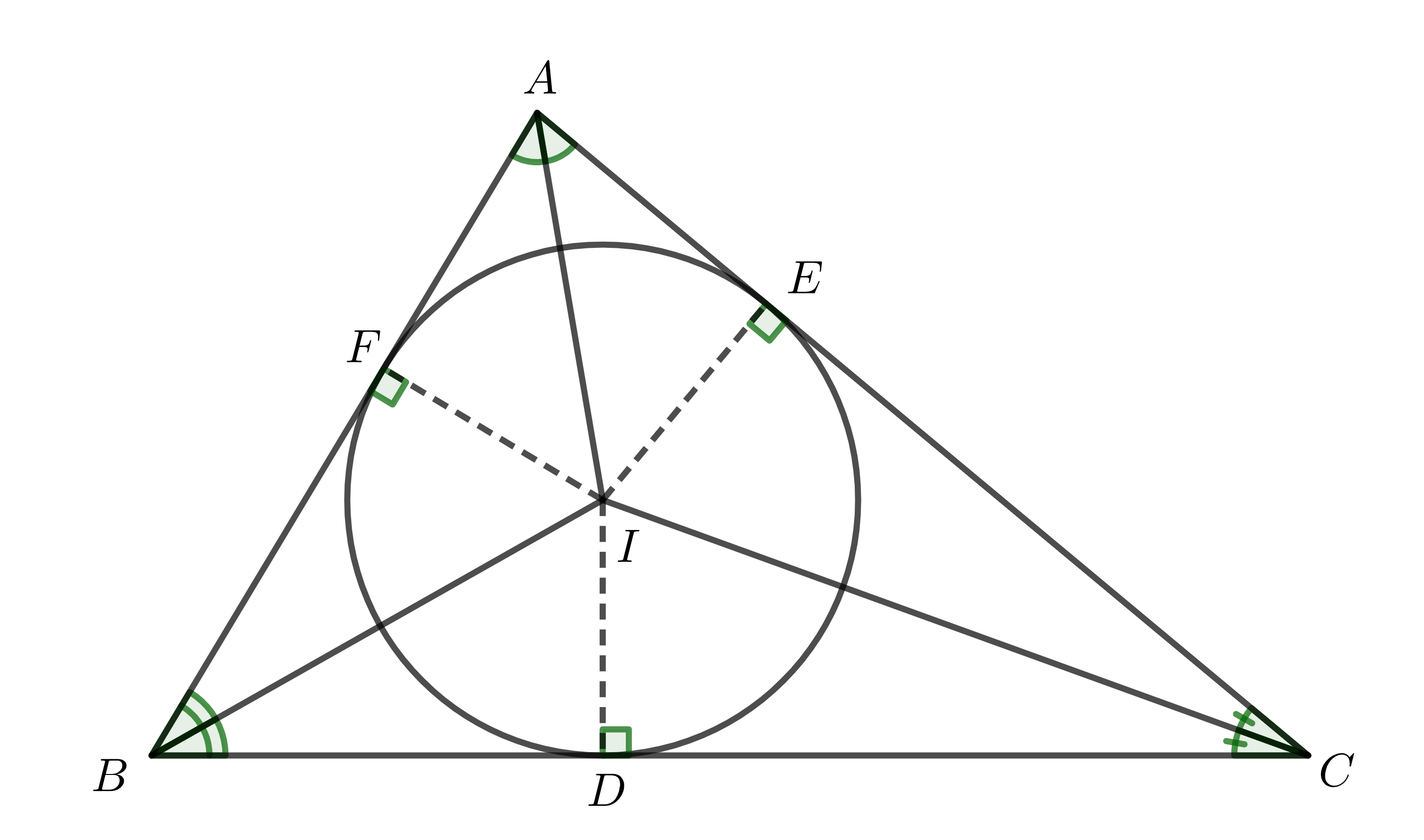
Dễ dàng chứng minh được \(ID=IE=IF=r\). Khi đó, đường tròn \(\left(I;r\right)\) là đường tròn nội tiếp tam giác \(ABC\), còn tam giác \(ABC\) ngoại tiếp đường tròn \(I\).
Chú ý: Mỗi tam giác chỉ có duy nhất một đường tròn nội tiếp.
@374926@@374988@
3. Đường tròn bàng tiếp tam giác
- Đường tròn bàng tiếp tam giác là đường tròn tiếp xúc với một cạnh tam giác và tiếp xúc với các phần kéo dài của hai cạnh còn lại.
- Tâm của đường tròn bàng tiếp là giao điểm một đường phân giác trong và một đường phân giác ngoài (hoặc giao điểm của hai đường phân giác ngoài) của tam giác.
Cụ thể: Cho tam giác \(ABC\). Gọi \(K\) là giao điểm hai đường phân giác ngoài của các góc \(B,C\). Gọi \(D,E,F\) lần lượt là chân đường vuông góc kẻ từ \(K\) đến các cạnh \(BC,AC,AB\).

Dễ dàng chứng minh được \(KD=KE=KF=r'\), đồng thời \(KA\) là phân giác của góc \(BAC\). Khi đó, \(\left(K;r'\right)\) là đường tròn bàng tiếp của \(\Delta ABC\).
Trong hình trên, đường tròn \(\left(K;r'\right)\) là đường tròn bàng tiếp trong góc \(A\). Mỗi góc của tam giác \(ABC\) đều có một đường tròn bàng tiếp.
Chú ý: Mỗi tam giác có ba đường tròn bàng tiếp.
@375079@@375163@