Bài 7: Ví trí tương đối của hai đường tròn
Nội dung lý thuyết
1. Ba vị trí tương đối của hai đường tròn
Căn cứ vào số điểm chung, ta có 3 vị trí tương đối của hai đường tròn phân biệt:
a) Hai đường tròn cắt nhau
- Nếu hai đường tròn có hai điểm chung thì chúng được gọi là hai đường tròn cắt nhau.
- Hai điểm chung đó được gọi là hai giao điểm.
- Đoạn nối hai giao điểm được gọi là dây chung.
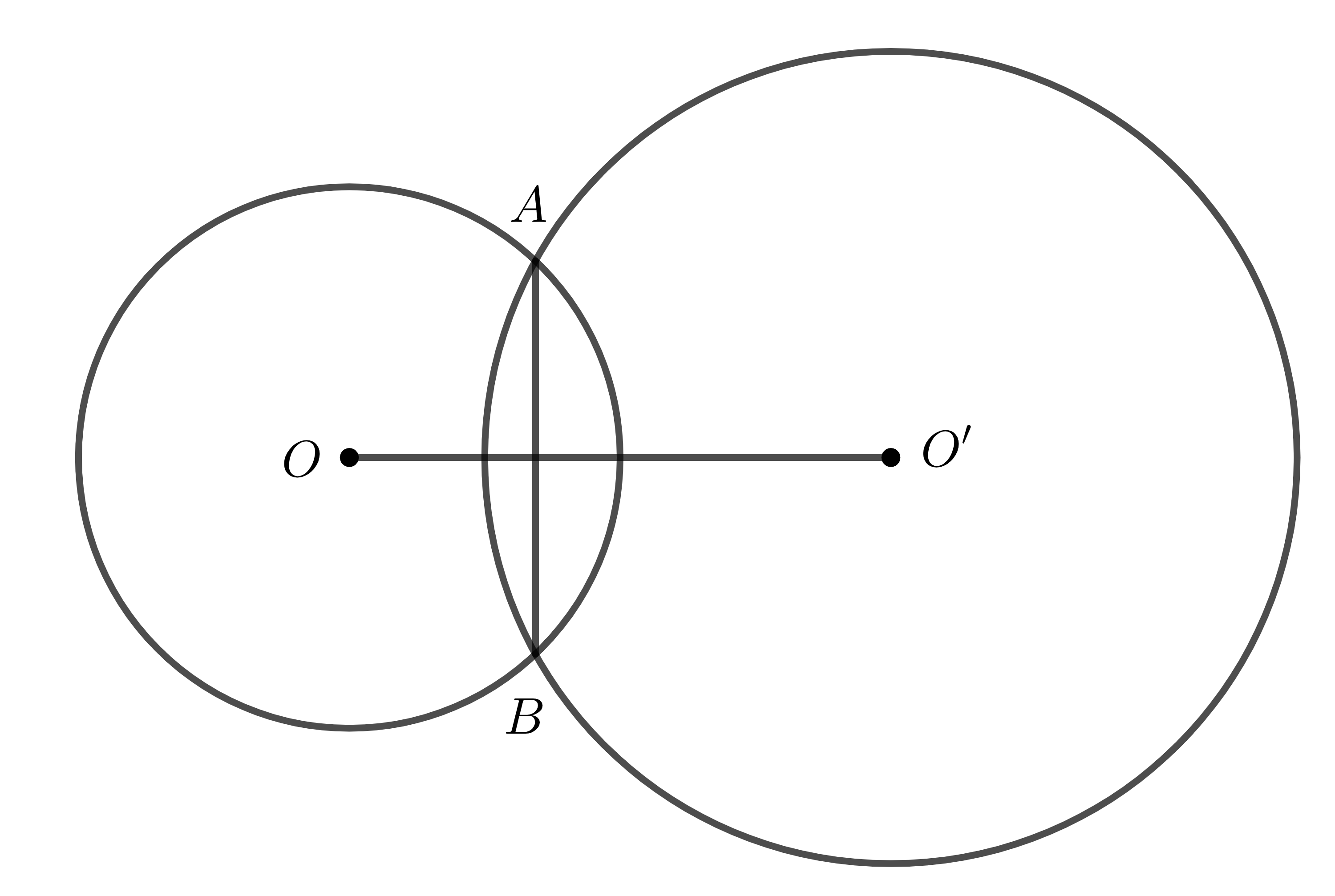
Cụ thể, trong hình 1 phía trên, hai đường tròn \(\left(O\right);\left(O'\right)\) cắt nhau tại hai giao điểm \(A,B\). Đoạn \(AB\) là dây chung.
b) Hai đường tròn tiếp xúc nhau
- Nếu hai đường tròn chỉ có một điểm chung thì chúng được gọi là hai đường tròn tiếp xúc nhau.
- Điểm chung được gọi là tiếp điểm.
- Hai đường tròn tiếp xúc nhau có thể rơi vào một trong hai trường hợp ứng với các hình sau:
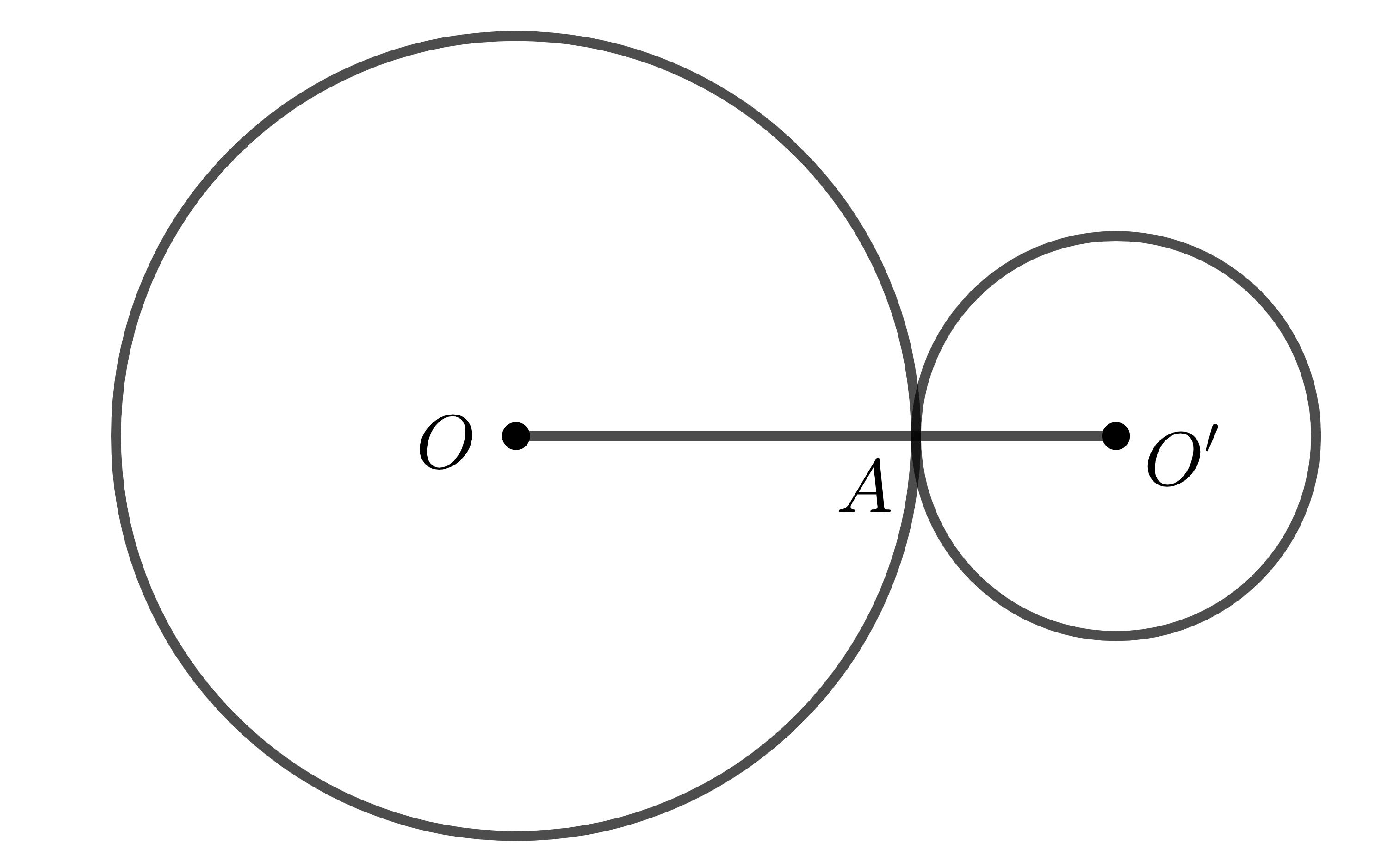
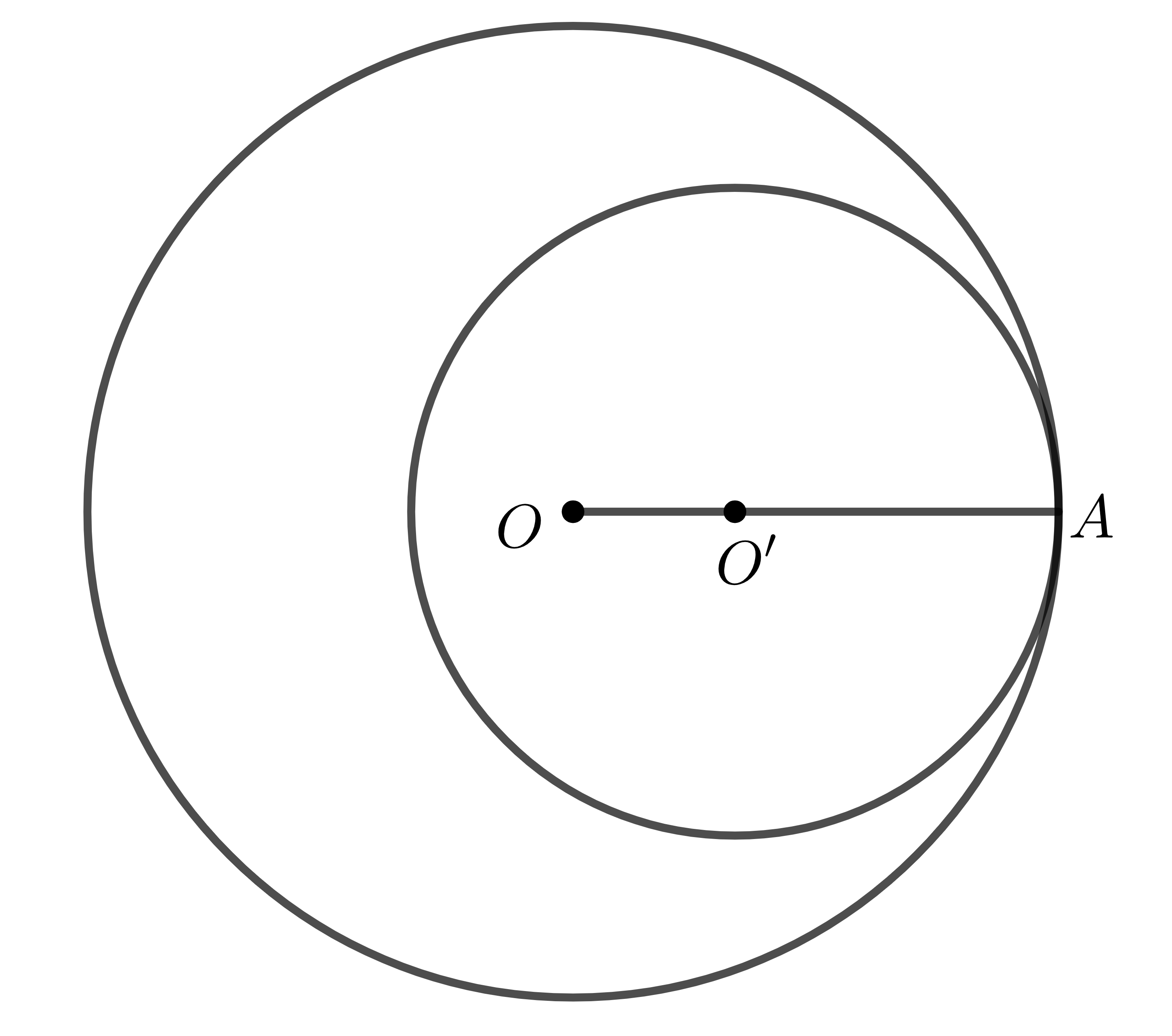
Cụ thể, trong hình 2 và hình 3 phía trên, hai đường tròn \(\left(O\right),\left(O'\right)\) tiếp xúc nhau tại tiếp điểm \(A\).
c) Hai đường tròn không giao nhau
- Nếu hai đường tròn không có điểm chung thì chúng được gọi là hai đường tròn không giao nhau.
- Hai đường tròn không giao nhau có thể rơi vào một trong hai trường hợp ứng với các hình sau:

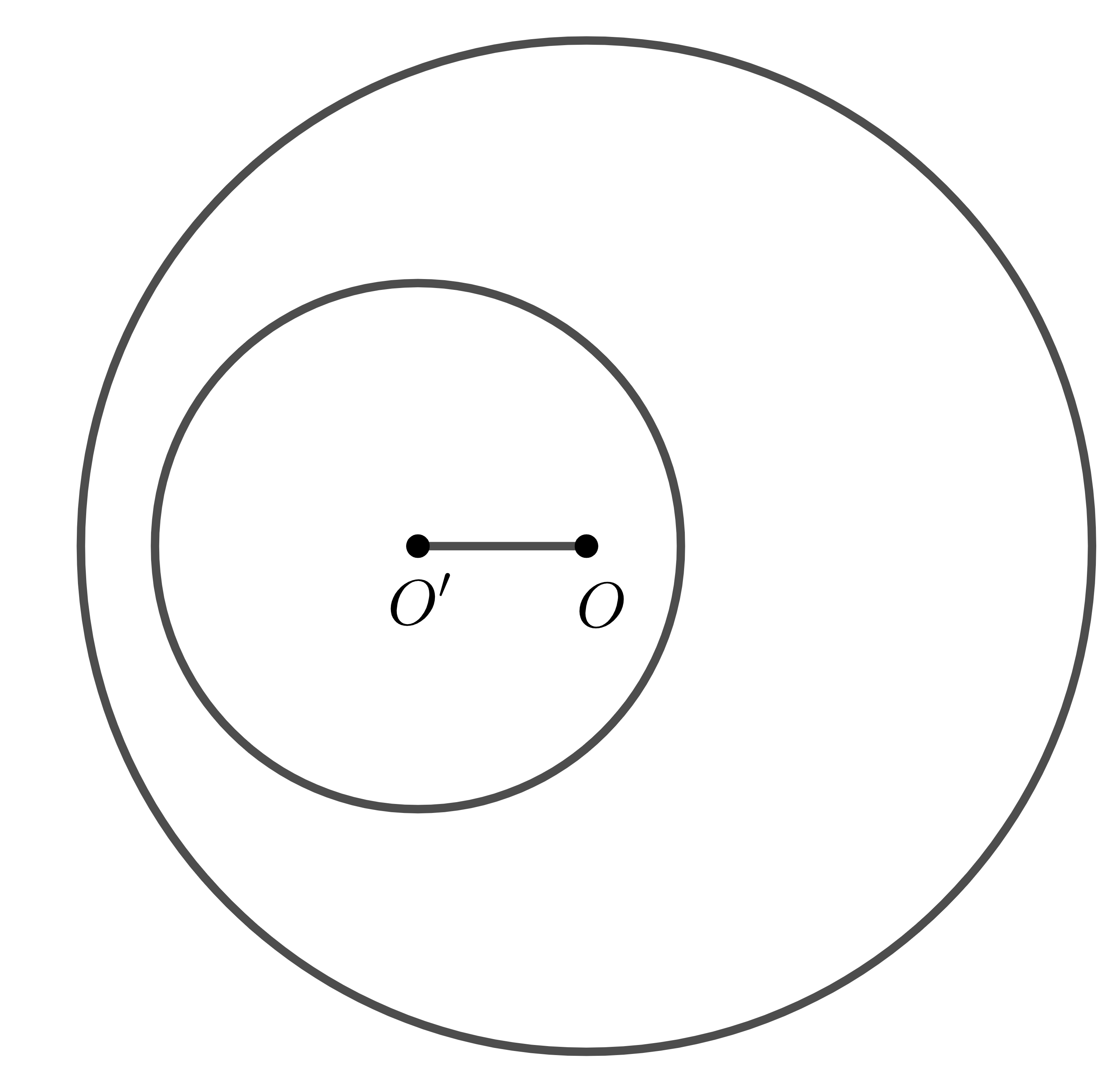
@383299@@383356@@383418@
2. Tính chất đường nối tâm
- Cho hai đường tròn \(\left(O\right),\left(O'\right)\) có tâm không trùng nhau. Khi đó, đường thẳng \(OO'\) gọi là đường nối tâm, đoạn thẳng \(OO'\) gọi là đoạn nối tâm.
- Do đường kính là trục đối xứng của mỗi đường tròn nên đường nối tâm là trục đối xứng của hình gồm hai đường tròn đó.
- Quan sát lại hình 1, ta thấy: Khi hai đường tròn \(\left(O\right),\left(O'\right)\) cắt nhau tại \(A,B\) ta có:
\(OA=OB\) nên \(O\) thuộc đường trung trực của \(AB\).
\(O'A=O'B\) nên \(O'\) thuộc đường trung trực của \(AB\)
\(\Rightarrow OO'\) chính là đường trung trực của đoạn thẳng \(AB\).
- Quan sát các hình 2 và 3, ta có thể dự đoán: Khi hai đường tròn \(\left(O\right),\left(O'\right)\) tiếp xúc nhau tại \(A\) thì điểm \(A\) nằm trên đường thẳng \(OO'\).
Từ đây, ta có định lí:
Định lí:
- Nếu hai đường tròn cắt nhau thì hai giao điểm đối xứng nhau qua đường nối tâm, tức là đường nối tâm là đường trung trực của dây chung.
- Nếu hai đường tròn tiếp xúc nhau thì tiếp điểm nằm trên đường nối tâm.
Ví dụ: Cho hai đường tròn \(\left(O\right);\left(O'\right)\) cắt nhau tại hai điểm \(A,B\). Kẻ các đường kính \(AC\) của \(\left(O\right)\) và \(AD\) của \(\left(O'\right)\) (hình vẽ).
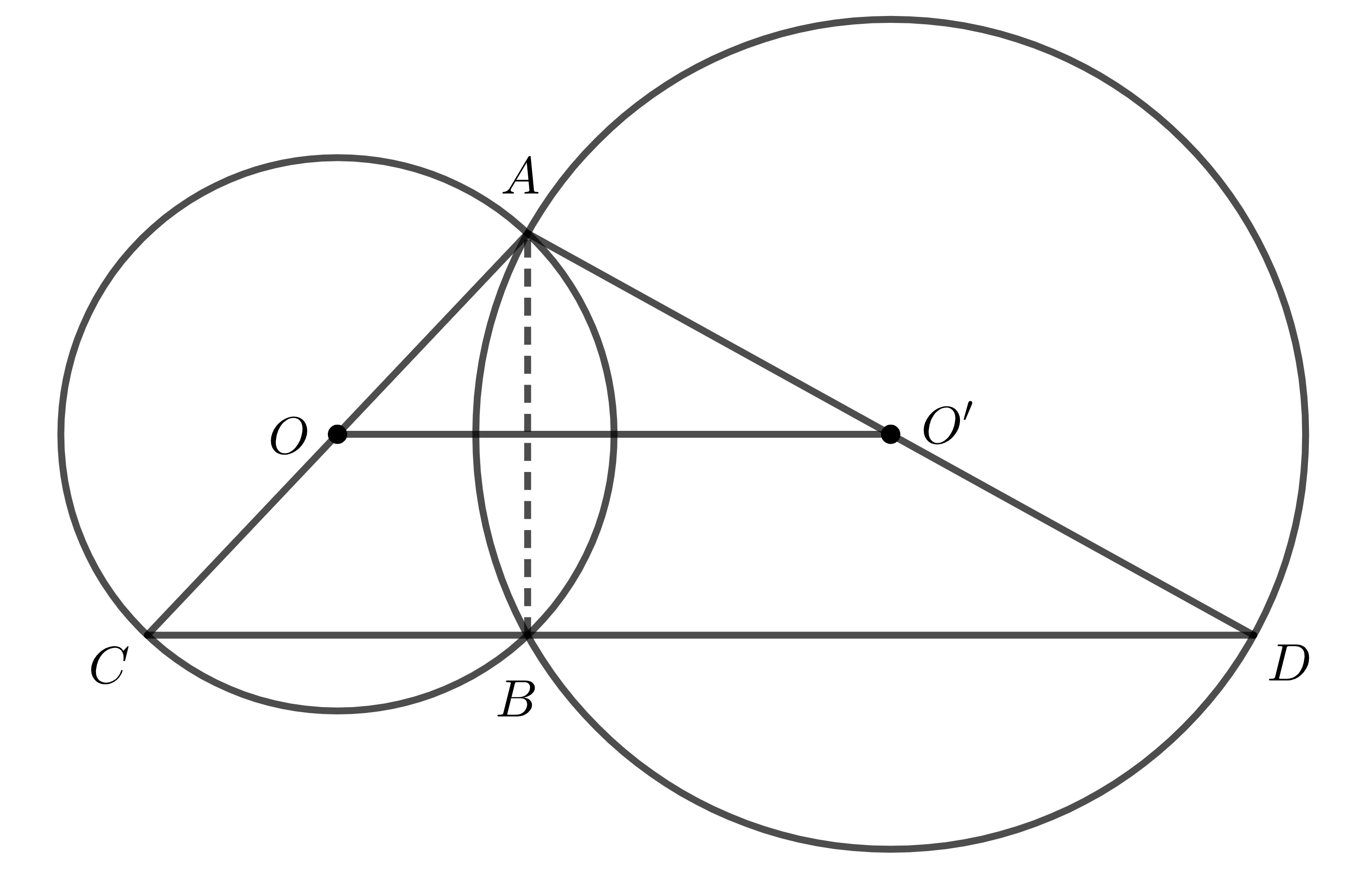
Chứng minh \(BC\) song song \(OO'\) và ba điểm \(B,C,D\) thẳng hàng.
Lời giải:
Hai đường tròn \(\left(O\right),\left(O'\right)\) cắt nhau tại các giao điểm \(A,B\)
\(\Rightarrow OO'\) là đường trung trực của \(AB\) hay \(OO'\perp AB\).
Lại có: \(AC\) là đường kính của đường tròn \(\left(O\right)\) \(\Rightarrow OB=\dfrac{1}{2}AC\)
Mà \(OB\) là trung tuyến ứng với cạnh \(AC\) của tam giác \(ABC\)
\(\Rightarrow\Delta ABC\) vuông tại \(B\) \(\Rightarrow BC\perp AB\).
Do đó, \(BC\) song song \(OO'\).
Chứng minh tương tự ta cũng có \(BD\) song song \(OO'\).
\(\Rightarrow B,C,D\) là 3 điểm thẳng hàng.
@383507@@57407@@57409@