1: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
Suy ra: góc AEF=góc AHF=góc C(1)
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>góc MAC=góc MCA(2)
Từ (1) và (2) suy ra góc AEF=góc C
2: Tham khảo:
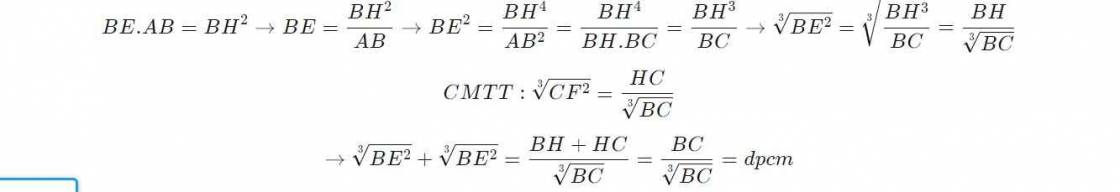
1: Xét tứ giác AEHF có góc AEH=góc AFH=góc FAE=90 độ
nên AEHF là hình chữ nhật
Suy ra: góc AEF=góc AHF=góc C(1)
Ta có: ΔABC vuông tại A
mà AM là đường trung tuyến
nên MA=MC
=>góc MAC=góc MCA(2)
Từ (1) và (2) suy ra góc AEF=góc C
2: Tham khảo:
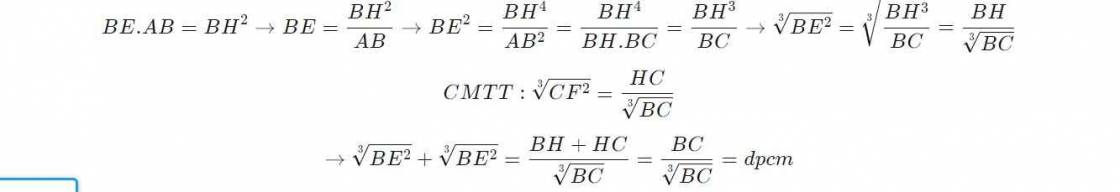
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H trên AB, AC. Chứng minh:
a) \(BC^2=3AH^2+BE^2+CF^2\)
b) \(\dfrac{AB^3}{AC^3}=\dfrac{BE}{CF}\)
Cho tam giác ABC vuông tại A đường cao AH. Gọi EF theo thứ tự là hình chiếu của H trên AB AC
A) Chứng minh \(BC=AB\cdot sinC+AC\cdot cosC\)
B) Chứng mình \(AF\cdot AC^2=EF\cdot BC\cdot AE\)
C)Chứng minh\(AH^3=BC\cdot BE\cdot CF=BC\cdot AE\cdot AF\)
1. Cho tam giác ABC vuông tại A có AH vuông góc với BC . Cạnh HE , HF là đường cao của tam giác AHB và tam giác AHC
a) Chứng minh BC2 = 3AH2 + BE2 + CF2
b) Cho BC = 2a cố định . Tìm GTNN của BE2 + CF2
c) Chứng minh BE2 =BH3 / BC
2. Cho tam giác ABC , có AH vuông góc với BC . Gọi E , F lần lượt là hình chiếu của H trên AB , AC . Biết AH = x , BC = 2a
a) Chứng minh AH3 = BC . BE . CF = BC . HE . HF
b) Tính diện tích tam giác AEF theo a và x . Tìm x để diện tích tam giác AEF đạt GTLN
cho tam giác ABC vuông tại A có đường cao AH. Gọi M,N lần lượt là hình chiếu của H trên AB và AC. Chứng minh: 1) BM^2 =BH^3/BC
2)AH^3= BC. BM . CN
3) HM . HN =AH^3/BC
Cho tam giác ABC vuông tại A, đường cao AH. Gọi E, F lần lượt là hình chiếu của H lên AB, AC.
a) Chứng minh: AE.AB = AF.AC và \(\widehat{AEF}=\widehat{ABC}\)
b) Đường trung tuyến AI của tam giác ABC cắt EF tại K. Chứng minh rằng \(cos^2B.sinB=\dfrac{KF}{BC}\)
Cho tam giác ABC vuông tại A, đường cao AH, AB=3cm, BC=6cm. 1) Giải tam giác ABC 2) Gọi E, F lần lượt là hình chiếu của H trên cạnh AB và AC. a) Tính độ dài AH và chứng minh: EF=AH b) Tính: EA.EB+AF.FC
Cho tg ABC vuông tại A, đường cao AH. Gọi EF lần lượt là hình chiếu của H trên AB, AC. CMR:
a) \(\dfrac{AH^2}{AC^2}=\dfrac{HB}{HC}\)
b) \(\dfrac{AB^3}{AC^3}=\dfrac{BE}{CE}\)
c) \(\sqrt[3]{BE^2}=\sqrt[3]{FC^2}+\sqrt[3]{BE^2}\)
d) \(BC^2=3AH^2+BE^2+CF^2\)
e) \(EF^3=BE.CF.BC\)
c) Chứng minh: \(tan^3C=\dfrac{BE}{CF}\)
Cho ∆ABC vuông tại A, đường cao AH.Gọi E,F lần lượt là hình chiếu của H lên AB,AC
a) Chứng minh AB*AE=AF*AC
b) Chứng minh AH^2=BC*BE*CF