\(MK=\dfrac{1}{2}DF=FM\) (trung tuyến ứng với cạnh huyền trong tam giác vuông DKF)
\(\Rightarrow\Delta FMK\) cân \(\Rightarrow\widehat{FKM}=\widehat{KFM}\)
\(\widehat{KFM}=\widehat{DBH}\) (cùng chắn cung DH của đường tròn ngoại tiếp BDHF)
\(\widehat{DBH}=\widehat{HFE}\) (cùng chắn cung ED của đường tròn ngoại tiếp BCEF)
\(\Rightarrow\widehat{FKM}=\widehat{HFE}\Rightarrow MK||EF\)
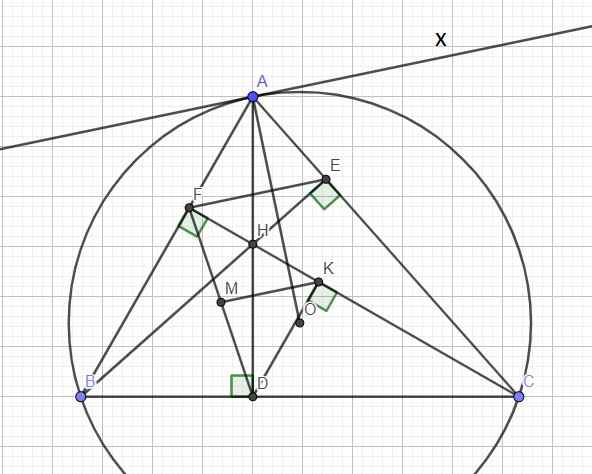
Dựng tiếp tuyến Ax của đường tròn (O)
\(\widehat{CAx}=\widehat{ABC}\) (cùng chắn cung AC của (O))
\(\widehat{ABC}+\widehat{CEF}=180^0\)(tứ giác BCEF nội tiếp)
\(\Rightarrow\widehat{AEF}=\widehat{ABC}\) (cùng bù \(\widehat{CEF}\))
\(\Rightarrow\widehat{AEF}=\widehat{CAx}\)
\(\Rightarrow EF||Ax\)
\(\Rightarrow MK||Ax\)
Mà \(Ax\perp OA\Rightarrow MK\perp OA\)