Ta có : Góc DAB = góc CAE = 90 độ => góc DAB + góc BAC = góc CAE + góc BAc
hay góc DAC = góc EAB
Xét tam giác ADC và tam giác ABE có :
AD = AB ; AC = AE ; góc DAC = góc EAB
=> tam giác ADC = tam giác ABE => DC = BE
Vì tam giác ADC = tam giác ABE nên góc AEB = góc ACD
mà góc AKE = góc BKC (đối đỉnh) , góc AKE + góc AEB = 90 độ
=> góc BKC + góc AEB = 90 độ hay góc BKC + góc ACD = 90 độ
=> góc DC vuông góc BE
Vì góc DAB=góc EAC => DÂB + BÂC = EÂC + BÂC
=> tam giác ADC = tam giác ABE (c.g.c)
=> DC = BE (dpcm)
+) tam giác AEK ( Â = 90 độ )
=> góc AEK + góc AKE = 90 độ
mà Góc AKE = góc BKC ( đ đỉnh ) và góc ACD = góc AEK ( tam giác ADC = tam giác AEB )
nên góc BKC + góc AcD = 90 độ
=> DC vuông góc với BE ( đpcm )
đây là câu trả lời của mình:
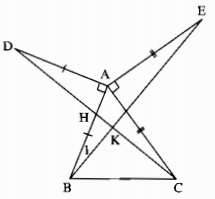
a) Xét ∆ABE và ∆ACD, ta có:
AB = AD (gt)
AE = AC (gt)
BAE^=BAC^+90∘CAD^=BAC^+90∘⇒BAE^=CAD^
Suy ra: ∆ABE = ∆ADC (c.g.c)
DC = BE (2 cạnh tương ứng)
b) Gọi giao điểm DC và AB là H, giao điểm của CD và BE là K
Ta có: ∆ABE = ∆ADC (chứng minh trên)
ABE^=D^ (1)
Trong tam giác vuông AHD, ta có: HAD^=90∘
⇒D^+AHD^=90∘ (tính chất tam giác vuông) (2)
Mà: AHD^=KHB^ (đối đỉnh) (3)
Từ (1), (2) và (3) suy ra: ABE^+KHB^=90∘
Trong ∆KHB, ta có:
KHB^+ABE^+BKH^=180∘ (tổng 3 góc trong tam giác)
⇒BKH^=180∘–(ABE^+BKH^)=180∘–90∘=90∘
Vậy DC⊥BE.
















