Question

cho tam giác ABC có góc B; góc C nhọn, đường cao AH

a) Chứng minh: AH=\(\dfrac{BC}{cotB+cotC}\)

b) Tính S_ABC, biết BC=4cm; góc B=45⁰; góc C=30⁰

Answer 1

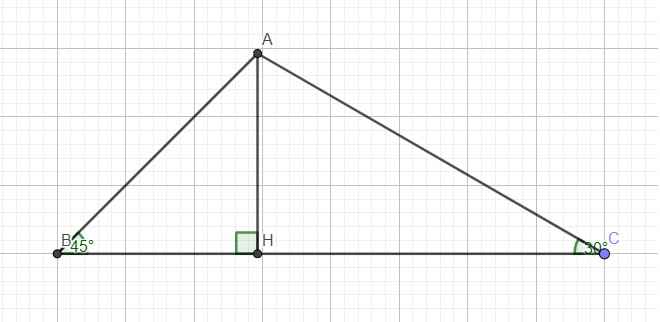
a.

Trong tam giác vuông ABH ta có:

\(cotB=\dfrac{BH}{AH}\Rightarrow BH=AH.cotB\)

Trong tam giác vuông ACH ta có:

\(cotC=\dfrac{CH}{AH}\Rightarrow CH=AH.cotC\)

\(\Rightarrow BH+CH=AH.cotB+AH.cotC\)

\(\Leftrightarrow BC=AH\left(cotB+cotC\right)\)

\(\Leftrightarrow AH=\dfrac{BC}{cotB+cotC}\) (đpcm)

b. Áp dụng công thức câu a:

\(AH=\dfrac{4}{cot45^0+cot30^0}=-2+2\sqrt{3}\) (cm)

\(S_{ABC}=\dfrac{1}{2}AH.BC=\dfrac{1}{2}.\left(-2+2\sqrt{3}\right).4=-4+4\sqrt{3}\approx2,93\left(cm^2\right)\)

Answer 2