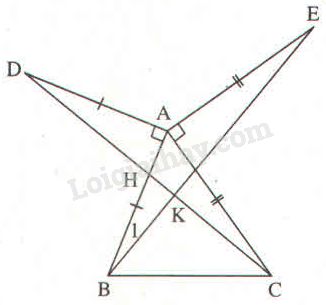
b) Gọi giao điểm của \(DC\) và \(AB\) là H, giao điểm của \(CD\) và \(BE\) là K.
Theo câu a) ta có \(\Delta ADC=\Delta ABE.\)
=> \(\widehat{ADC}=\widehat{ABE}\) (2 góc tương ứng) (1).
+ Vì \(\Delta AHD\) vuông tại \(A\left(gt\right)\)
=> \(\widehat{ADH}+\widehat{AHD}=90^0\) (tính chất tam giác vuông).
Hay \(\widehat{ADC}+\widehat{AHD}=90^0\) (2).
Mà \(\widehat{AHD}=\widehat{KHB}\) (vì 2 góc đối đỉnh) (3).
Từ (1), (2) và (3) => \(\widehat{ABE}+\widehat{KHB}=90^0.\)
Hay \(\widehat{HBK}+\widehat{KHB}=90^0.\)
+ Xét \(\Delta KHB\) có:
\(\widehat{KHB}+\widehat{HBK}+\widehat{BKH}=180^0\) ( định lí tổng 3 góc trong một tam giác).
=> \(90^0+\widehat{BKH}=180^0\)
=> \(\widehat{BKH}=180^0-90^0\)
=> \(\widehat{BKH}=90^0.\)
=> \(HK\perp BK\)
Hay \(DC\perp BE\left(đpcm\right).\)
Chúc bạn học tốt!
(tự vẽ hình nhé)
Xét tam giác ABD và tam giác ACE có:
góc DAB=góc EAC(=90 độ);AD=AB(gt);AE=AC(gt)
=>tam giác ABD=tam giác ACE(c.g.c)
=>AD=AE(2 cạnh tương ứng) và AB=AC(2 cạnh tương ứng)
Ta có AD+AC=AC;AB+AE=BE mà AD=AE;AB=AC=> DC=BE
Ta có: góc BAD + góc DAE =180 độ (2 góc kề bù)
=> góc DAE=90 độ

















