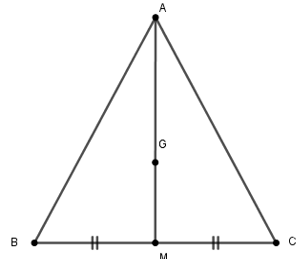
+ Vì \(AM\) là đường trung tuyến của \(\Delta ABC\left(gt\right)\)
=> \(M\) là trung điểm của \(BC.\)
=> \(BM=CM=\frac{1}{2}BC\) (tính chất trung điểm).
=> \(BM=CM=\frac{1}{2}.16=\frac{16}{2}=8\left(cm\right).\)
+ Xét \(\Delta ABC\) có:
\(AB=AC=17cm\left(gt\right)\)
=> \(\Delta ABC\) cân tại \(A.\)
Có \(AM\) là đường trung tuyến (gt).
=> \(AM\) đồng thời là đường cao của \(\Delta ABC.\)
=> \(AM\perp BC.\)
+ Xét \(\Delta ABM\) vuông tại \(M\left(cmt\right)\) có:
\(AM^2+BM^2=AB^2\) (định lí Py - ta - go).
=> \(AM^2+8^2=17^2\)
=> \(AM^2=17^2-8^2\)
=> \(AM^2=289-64\)
=> \(AM^2=225\)
=> \(AM=15\left(cm\right)\) (vì \(AM>0\)).
+ Vì G là trọng tâm của \(\Delta ABC\left(gt\right).\)
=> \(AG=\frac{2}{3}AM\) (tính chất trọng tâm của tam giác).
=> \(AG=\frac{2}{3}.15\)
=> \(AG=\frac{30}{3}\)
=> \(AG=10\left(cm\right).\)
Vậy \(AM=15\left(cm\right);AG=10\left(cm\right).\)
Chúc bạn học tốt!











