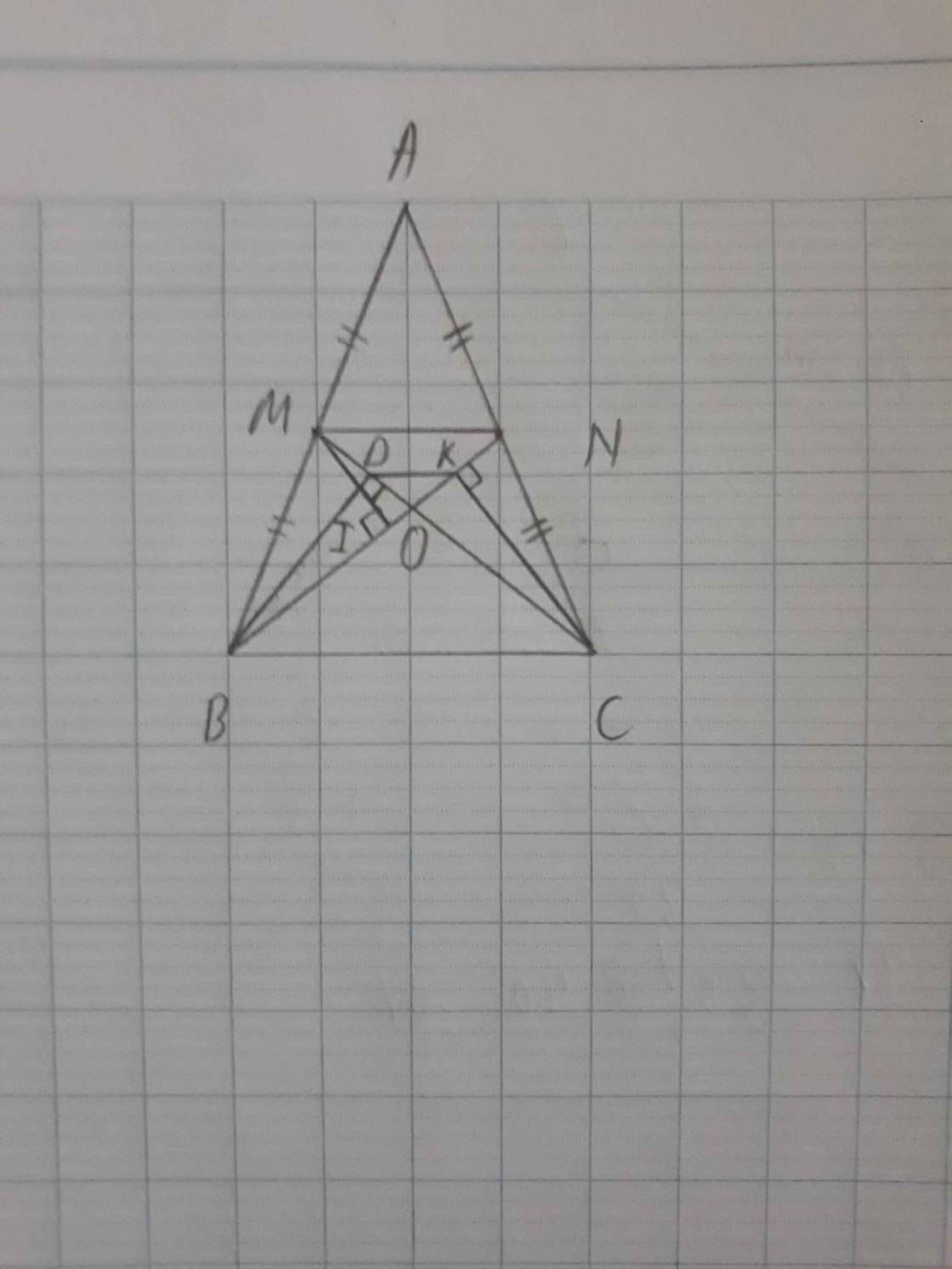
Cho tam giác ABC cân tại A (A <90°). Gọi M. N lần lượt là trung điểm của AB và AC.
a) Tính MN biết BC =7cm.
b) Chứng minh rằng tử giác MNCB là hình thang cân.
c) Kẻ MI vuông góc với BN tại I, (I thuộc BN) và CK vuông góc với BN tại K (K thuộc BN). Chứng minh rằng : CK=2MI.
d) Kẻ BD vuông góc với MC tại D (D thuộc MC). CMR: DK // BC
a) Ta có M là trung điểm của AB ; N là trung điểm của AC
=> MN là đường trung bình của ΔABC
\(=>MN=\dfrac{1}{2}BC=3,5cm\) ; MN // BC
b) MN // BC (cmt) => BMNC là hình thang
mà \(\widehat{MBC}=\widehat{NCB}\) (ΔABC cân)
=> BMNC là hình thang cân
c) Gọi giao điểm BN và CM là O
BMNC là hình thang cân => OM = ON ; OB = OC
Ta có MN // BC \(=>\dfrac{MO}{OC}=\dfrac{MN}{BC}=\dfrac{1}{2}\)
=> MI // CK \(=>\dfrac{MI}{CK}=\dfrac{MO}{OC}=\dfrac{1}{2}=>CK=2MI\)
d) Xét Δ vuông OBD là Δ vuông OCK có
OB = OC (gt)
\(\widehat{BOD}=\widehat{COK}\) (2 góc đối đỉnh)
=> ΔOBD = ΔOCK
=> OD = OK \(=>\dfrac{OD}{OC}=\dfrac{OK}{OB}\) => OK // BC