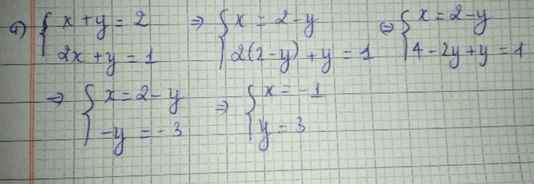a. Thay m=2 vào hệ phương trình, ta có: \(\left\{{}\begin{matrix}x+y=2\\2x+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\y=3\end{matrix}\right.\)
b. Phương trình tọa độ giao điểm của phương trình 1 và (P) là: \(m-x=-2x^2\)
\(\Leftrightarrow2x^2-x+m=0\) (*)
Để phương trình có nghiệm thì \(\Delta\ge0\Leftrightarrow1-4.2m\ge0\Leftrightarrow m\le\dfrac{1}{8}\)
Phương trình tọa độ giao điểm của phương trình 2 và (P) là: \(1-mx=-2x^2\)
\(\Leftrightarrow2x^2-mx+1=0\)
Để phương trình có nghiệm thì \(\Delta\ge0\Leftrightarrow m^2-4.2\ge0\Leftrightarrow\left[{}\begin{matrix}m\le-2\sqrt{2}\\m\ge2\sqrt{2}\end{matrix}\right.\)
Mà cả 3 đường thẳng cắt chung 1 điểm nên \(2x^2-x+m=2x^2-mx+1\)
\(\Leftrightarrow-x+m=-mx+1\)
\(\Leftrightarrow-x+mx+m-1=0\)
\(\Leftrightarrow m\left(x+1\right)-\left(x+1\right)=0\)
\(\Leftrightarrow\left(m-1\right)\left(x+1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}m=1\\x=-1\end{matrix}\right.\)
Khi m=1 thì phương trình 1: x+y=1, phương trình 2: x+y=1 là hai đường thẳng trùng nhau, đồng thời m KTM (loại)
Thay x=-1 vào (*) ta được: \(2\left(-1\right)^2-\left(-1\right)+m=0\Leftrightarrow m=-3\)
Phương trình 1: x+y=-3, phương trình 2: -3x+y=1 (TM)
Thay m=2
pt: \(\left\{{}\begin{matrix}x+y=2\\2x+y=1\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}x=-1\\2x+y=1\end{matrix}\right.\)
\(\Leftrightarrow-2+y=1\)
\(\Leftrightarrow y=3\)