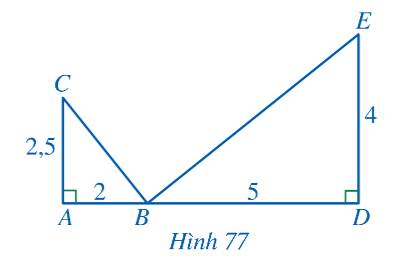
a) Ta có:
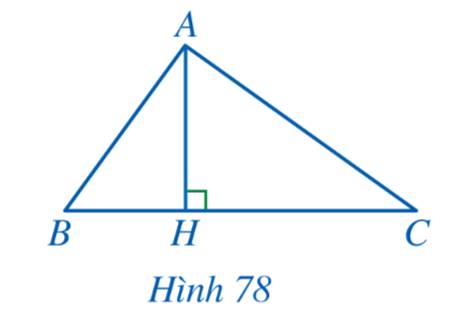
\(A{H^2} = BH.CH \Rightarrow AH.AH = BH.CH \Rightarrow \frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\)
Xét tam giác HAB và tam giác HCA có:
\(\frac{{AH}}{{CH}} = \frac{{BH}}{{AH}}\) và \(\widehat {AHB} = \widehat {CHA} = 90^\circ \)
\( \Rightarrow \Delta HAB \backsim \Delta HCA\) (c-g-c)
b) Vì \(\Delta HAB \backsim \Delta HCA\) nên \(\widehat {HBA} = \widehat {HAC}\)
Xét tam giác AHB vuông tại H có:
\(\begin{array}{l}\widehat {HAB} + \widehat {HBA} = 90^\circ \\ \Rightarrow \widehat {HAB} + \widehat {HAC} = 90^\circ \\ \Rightarrow \widehat {BAC} = 90^\circ \end{array}\)
Vậy tam giác ABC vuông tại A.