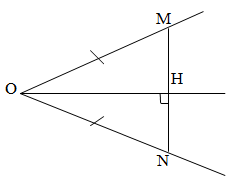
a, Ta có:OM=ON\(\Rightarrow\Delta\)OMN cân tại O\(\Rightarrow\widehat{OMN}=\widehat{ONM}\)
Xét ΔOHM và ΔOHN có:
\(\widehat{OHN}=\widehat{OHM}\left(=90^o\right)\)
Chung OH
OM=ON(gt)
\(\Rightarrow\Delta OHM=\Delta OHN\left(ch-gn\right)\)
b, \(\Delta OHM=\Delta OHN\left(cma\right)\Rightarrow HM=HN\) (2 cạnh tương ứng)
a) Xét tam giác OHM vuông tại H và tam giác OHN vuông tại H ta có:
\(\widehat{H1}=\widehat{H2}\) \(\left(OH\perp MN\right)\)
OM = ON (kí hiệu giống nhau)
=> Tam giác OHM = tam giác OHN (ch-gn)
b) Ta có tam giác OHM = tam giác OHN => HM = HN (cạnh tương ứng)