Bài 1: Định lý Talet trong tam giác
Các câu hỏi tương tự
CHo hình thang ABCD(AB//CD), một đường thẳng sông song với 2 đáy, cắt AD và AC ở M và N sao cho MD=2MA
a) tính tỉ số \(\dfrac{NB}{NC}\)
b) CHo AB=8cm, CD=17cm, Tính MN
Cho hình thang ABCD có AB //CD và AB CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
Chứng minh rằng :
a) dfrac{MA}{AD}dfrac{NB}{BC}
b) dfrac{MA}{MD}dfrac{NB}{NC}
c) dfrac{MD}{DA}dfrac{NC}{CB}
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Đọc tiếp
Cho hình thang ABCD có AB //CD và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD, BC theo thứ tự tại M và N.
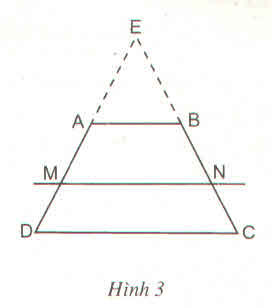
Chứng minh rằng :
a) \(\dfrac{MA}{AD}=\dfrac{NB}{BC}\)
b) \(\dfrac{MA}{MD}=\dfrac{NB}{NC}\)
c) \(\dfrac{MD}{DA}=\dfrac{NC}{CB}\)
Hướng dẫn : Kéo dài các tia DA, CB cắt nhau tại E (h.3), áp dụng định lí Ta - let trong tam giác và tính chất của tỉ lệ thức để chứng minh
Cho hình thang ABCD(AB//CD,ABCD).Có O là giao điểm của 2 đường chéo.Qua O kẻ 2 đường thẳng song song với 2 đáy cắt AD tại M,cắt BC tại N.a) So sánh các tỉ số OM/CD và AO/AC,ON/CD và OB/BD.b) Chứng minh OMON.c) Tính MN biết AB4cm CD6cm.d) Gọi E là giao điểm của 2 đường thẳng AD và BC.Chứng minh E,O và trung điểm của BC thẳng hàng.e) Qua B kẻ đường thẳng song song với AD cắt AC tại K. Chứng minh OA mũ 2 OK*OC
Đọc tiếp
Cho hình thang ABCD(AB//CD,AB<CD).Có O là giao điểm của 2 đường chéo.Qua O kẻ 2 đường thẳng song song với 2 đáy cắt AD tại M,cắt BC tại N.
a) So sánh các tỉ số OM/CD và AO/AC,ON/CD và OB/BD.
b) Chứng minh OM=ON.
c) Tính MN biết AB=4cm CD=6cm.
d) Gọi E là giao điểm của 2 đường thẳng AD và BC.Chứng minh E,O và trung điểm của BC thẳng hàng.
e) Qua B kẻ đường thẳng song song với AD cắt AC tại K. Chứng minh OA mũ 2 = OK*OC
. Cho hình thang ABCD (AB // CD). Đường thẳng song song hai đáy cắt cạnh AD tại M, cắt cạnh BC tại N sao cho MD = 3MA. a) Tính tỉ số NB NC . b) Cho AB = 8cm, CD = 20cm. Tính MN.
cho hình thang ABCD có AB//CD và AB<CD.Một đường thẳng a song song với các cạnh đấy AB,CD và cắt các cạnh bên AD,BC thứ tự tại M và N.Chứng minh rằng:
a)MA/AD=NB/BC
b)MA/MD=NB/NC
c)MD/AD=NC/BC
Cho hình thang ABCD (AB // CD). Đường thẳng song song hai đáy cắt cạnh AD tại M, cắt cạnh BC tại N sao cho MD = 3MA. a) Tính tỉ số \(\frac{NB}{NC}\)
b) Cho AB = 8cm, CD = 20cm. Tính MN
Cho hình thang ABCD (AB // CD) và AB < CD. Đường thẳng song song với đáy AB cắt các cạnh bên AD , BC theo thứ tự tại M, N. Chứng minh rằng: a) MA NB AD BC = b) MA NB MD NC = c) MD NC DA CB = Hướng dẫn: Kéo dài các tia DA và CB cắt nhau tại E, áp dụng định lý Ta – lét trong tam giác và tính chất tỉ lệ thức để chứng minh
giúp mik với thanks nhiều nha:))
Cho tam giác ABC, trên AB, AC lần lượt lấy 2 điểm M và N. Biết AM=3cm, MB=2cm, AN=7,5cm, NC=5cm.
a. Chứng minh MN//BC?
b. Gọi I là trung điểm BC, AI giao MN=K. Cmr: K là trung điểm của NM?
Xem chi tiết
Bài 1:Cho tam giác ABC có M,I lần lượt là trung điểm của BC,AM. Gọi K là giao điểm của CI và AB. Tính dfrac{AK}{AB}
Bài 2: Cho hình bình hành ABCD. Gọi M,N lần lượt là các điểm thuộc cạnh AB,AD sao cho dfrac{AM}{AB}dfrac{AN}{AD}k
a. Chứng minh rằng AC,BN,DM đồng quy
b. Gọi E,F lần lượt là giao điểm của MC và AD;NC và AB
Chứng minh rằng EF// MN. Tính dfrac{EF}{MN}
Đọc tiếp
Bài 1:Cho tam giác ABC có M,I lần lượt là trung điểm của BC,AM. Gọi K là giao điểm của CI và AB. Tính \(\dfrac{AK}{AB}\)
Bài 2: Cho hình bình hành ABCD. Gọi M,N lần lượt là các điểm thuộc cạnh AB,AD sao cho \(\dfrac{AM}{AB}\)=\(\dfrac{AN}{AD}\)=k
a. Chứng minh rằng AC,BN,DM đồng quy
b. Gọi E,F lần lượt là giao điểm của MC và AD;NC và AB
Chứng minh rằng EF// MN. Tính \(\dfrac{EF}{MN}\)










